题目内容
若f（x）=2f′（1）x2-3x，那么f′（2）= ．
考点：导数的运算
专题：导数的概念及应用
分析：利用求导法则，求导，先求f′（1），然后代入值即可，注意f′（1）是一个常数．
解答：
解：∵f（x）=2f′（1）x2-3x，
∴f′（x）=4f′（1）x-3，
令x=1，
∴f′（1）=4f′（1）-3，
∴f′（1）=1．
∴f′（x）=4x-3，
∴f′（2）=4×2-3=5，
故答案为：5．
∴f′（x）=4f′（1）x-3，
令x=1，
∴f′（1）=4f′（1）-3，
∴f′（1）=1．
∴f′（x）=4x-3，
∴f′（2）=4×2-3=5，
故答案为：5．
点评：本题考查学生灵活运用求导法则求函数的导函数，f′（1）是一个常数，是一道中档题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
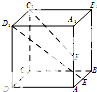已知点E，F分别是正方体ABCD-A1B1C1D1的棱AB，AA1的中点，点M，N分别是线段D1E与C1F上的点，则与平面ABCD垂直的直线MN有（ ）设f0（x）=sinx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x），n∈N，则f2015（x）=（ ）
| A、sinx | B、-sinx |
| C、cosx | D、-cosx |