题目内容
某校高中生共有2000人,其中高一年级600人,高二年级640人,调查选修课选学情况,现采用分层抽样的方法,抽取一个容量为50的样本,那么高三年级抽取人数为( )
| A、15 | B、16 | C、18 | D、19 |
考点:分层抽样方法
专题:概率与统计
分析:先求出每个个体被抽到的概率,再用每层的个体数乘以每个个体被抽到的概率就等于该层应抽取的个体数.
解答:
解:每个个体被抽到的概率等于
=
,
∴高三年级抽取人数为:(2000-600-640)×
=19人.
故选:D.
| 50 |
| 2000 |
| 1 |
| 40 |
∴高三年级抽取人数为:(2000-600-640)×
| 1 |
| 40 |
故选:D.
点评:本题主要考查分层抽样的定义和方法,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数,属于基础题.

练习册系列答案
相关题目
已知不等式
<0的解集为P,若x0∈P,则“|x0|<1“的概率为( )
| x-5 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示的程序框图,输出的S值为( )


| A、1 | B、5 | C、14 | D、30 |
已知tan(x+
)=
,0<x<
,则
=( )
| π |
| 4 |
| 12 |
| 5 |
| π |
| 4 |
| cos2x | ||
sin(
|
A、
| ||
B、
| ||
C、
| ||
D、-
|
设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2015(x)=( )
| A、sinx | B、-sinx |
| C、cosx | D、-cosx |
已知函数f(x)定义域为R,对于定义域内任意x、y,都有f(x)+f(y)=f(x+y),且x>0时,f(x)<0,则( )
| A、f(x)是偶函数且在(-∞,+∞)上单调递减 |
| B、f(x)是偶函数且在(-∞,+∞)上单调递增 |
| C、f(x)是奇函数且在(-∞,+∞)上单调递减 |
| D、f(x)是奇函数且在(-∞,+∞)上单调递增 |

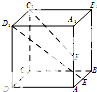 已知点E,F分别是正方体ABCD-A1B1C1D1的棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则与平面ABCD垂直的直线MN有( )
已知点E,F分别是正方体ABCD-A1B1C1D1的棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则与平面ABCD垂直的直线MN有( )