题目内容
6.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足2sin(A-$\frac{π}{3}$)=$\sqrt{3}$,sin(B-C)=4cosBsinC,则$\frac{b}{c}$等于( )| A. | 2$\sqrt{2}$+1 | B. | 2$\sqrt{2}$-1 | C. | $\sqrt{6}$+1 | D. | $\sqrt{6}$-1 |
分析 由2sin(A-$\frac{π}{3}$)=$\sqrt{3}$,运用三角函数公式求出A,sin(B-C)和与差公式打开,再由正余弦弦定理,即可得$\frac{b}{c}$的值
解答 解:由2sin(A-$\frac{π}{3}$)=$\sqrt{3}$,
可得:sin(A-$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$.
∵0<A<π
∴A=$\frac{2π}{3}$.
又∵sin(B-C)=sinBcosC-sinCcosB=4cosBsinC,
可得:sinBcosC=5cosBsinC.
得:sinBcosC+cosBsinC=6cosBsinC.
即sinA=6cosBsinC.
∴由正弦弦定理:得a=2c×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$.
得2a2+3c2-3b2=0,即${a}^{2}=\frac{3}{2}({b}^{2}+{c}^{2})$
由余弦弦定理:a2=b2+c2-2bc×cos(120°)=b2+c2+bc.
∴b2-2bc-5c2=0,
同时除以bc.
可得:$(\frac{b}{c})^{2}-2×\frac{b}{c}-5=0$.
解得:$\frac{b}{c}$=$\sqrt{6}+1$.
故选:C.
点评 本题考查三角形的余正弦定理和内角和定理以及和与差的运用,考查运算能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
2.已知全集U={x|y=log2(x-1)},集合A={x||x-2|<1},则∁UA=( )
| A. | (3,+∞) | B. | [3,+∞) | C. | (1,3) | D. | (-∞,1] |
1.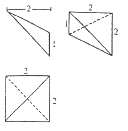 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $2\sqrt{3}$ |
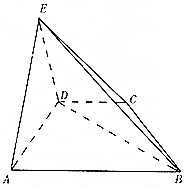 如图,在四棱锥E-ABCD中,△ADE是正三角形,侧面ADE⊥底面ABCD,AB∥DC,BD=2DC=4,AD=3,AB=5.
如图,在四棱锥E-ABCD中,△ADE是正三角形,侧面ADE⊥底面ABCD,AB∥DC,BD=2DC=4,AD=3,AB=5.