题目内容
2.已知全集U={x|y=log2(x-1)},集合A={x||x-2|<1},则∁UA=( )| A. | (3,+∞) | B. | [3,+∞) | C. | (1,3) | D. | (-∞,1] |
分析 先将A,U化简,再求CUA.
解答 解:全集U={x|y=log2(x-1)}=(1,+∞),
集合A={x||x-2|<1}={x|-1<x-2<1}={x|1<x<3}=(1,3),
则∁UA=[3,+∞),
故选:B
点评 本题考查集合的基本运算,属于基础题.

练习册系列答案
相关题目
12.运行如图所示的程序框图,则输出结果为( )
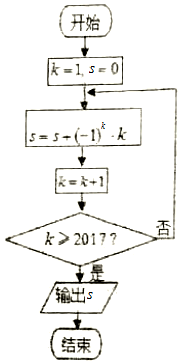

| A. | 2017 | B. | 2016 | C. | 1009 | D. | 1008 |
13.已知抛物线C:y2=4x的焦点为F,点P(2,t)为抛物线C上一点,则|PF|等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
6.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足2sin(A-$\frac{π}{3}$)=$\sqrt{3}$,sin(B-C)=4cosBsinC,则$\frac{b}{c}$等于( )
| A. | 2$\sqrt{2}$+1 | B. | 2$\sqrt{2}$-1 | C. | $\sqrt{6}$+1 | D. | $\sqrt{6}$-1 |
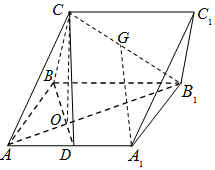 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且OC⊥平面ABB1A1.