题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤2}\\{lo{g}_{2}(x-1),x>2}\end{array}\right.$,则f(f(6))的值为log25-2.分析 利用分段函数直接求解函数值即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤2}\\{lo{g}_{2}(x-1),x>2}\end{array}\right.$,则f(f(6))=f(log2(6-1))=f(log25)
=f(log2($lo{g}_{2}\frac{5}{2}$-1))=f(log2(log2$\frac{5}{4}$))=${2}^{lo{g}_{2}(lo{g}_{2}\frac{5}{4})}$=log25-2.
故答案为:log25-2.
点评 本题考查分段函数的应用,函数的在的求法,考查计算能力.

练习册系列答案
相关题目
3.过平面区域$\left\{\begin{array}{l}{x-y+2≥0}\\{y+2≥0}\\{x+y+2≤0}\end{array}\right.$内一点作圆O:x2+y2=1的两条切线,切点分别为A、B,记∠APB=α,则当α最小时,cosα的值为( )
| A. | $\frac{9}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{\sqrt{5}}{20}$ | D. | $\frac{4}{5}$ |
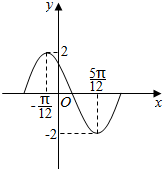 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$). 如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.
如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.