题目内容
在△ABC中,已知25cos2A+120sin2
=17.
(1)求cosA的值;
(2)若a=4
,b=5,求向量
在
方向上的投影.
| B+C |
| 2 |
(1)求cosA的值;
(2)若a=4
| 2 |
| BA |
| BC |
考点:余弦定理,平面向量数量积的运算
专题:解三角形
分析:(1)已知等式利用二倍角的余弦函数公式化简,整理后即可求出cosA的值;
(2)由cosA的值求出sinA的值,利用正弦定理求出sinB的值,进而确定出cosB的值,利用余弦定理求出c的值,即可求出向量
在
方向上的投影.
(2)由cosA的值求出sinA的值,利用正弦定理求出sinB的值,进而确定出cosB的值,利用余弦定理求出c的值,即可求出向量
| BA |
| BC |
解答:
解:(1)由25cos2A+120sin2
=17,得25cos2A+60[1-cos(B+C)]=17,
整理得:25cos2A+60cosA+43=0,即25cos2A+30cosA+9=0,
整理得:(5cosA+3)2=0,
解得cosA=-
;
(2)由(1)得sinA=
,
∴由正弦定理得:sinB=
=
,
∵a>b,∴B<A,
∴cosB=
,
由余弦定理得:cosB=
=
,
解得:c=1或c=7,
∵c<a,∴c=1,
则
在
上的投影为
=
=cosB=
.
| B+C |
| 2 |
整理得:25cos2A+60cosA+43=0,即25cos2A+30cosA+9=0,
整理得:(5cosA+3)2=0,
解得cosA=-
| 3 |
| 5 |
(2)由(1)得sinA=
| 4 |
| 5 |
∴由正弦定理得:sinB=
| bsinA |
| a |
| ||
| 2 |
∵a>b,∴B<A,
∴cosB=
| ||
| 2 |
由余弦定理得:cosB=
| 32+c2-25 | ||
8
|
| ||
| 2 |
解得:c=1或c=7,
∵c<a,∴c=1,
则
| BA |
| BC |
| ||||
|
|
| cacosB |
| a |
| ||
| 2 |
点评:此题考查了正弦、余弦定理,以及平面向量的数量积运算,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
设A={x||x-a|<1},B={x|(x-1)(5-x)>0},若A∩B=∅,则实数a的取值范围是( )
| A、{a|0≤a≤6} |
| B、{a|a≤2或a≥4} |
| C、{a|a≤0或a≥6} |
| D、{a|2≤a≤4} |
已知命题p:对任意x∈R,总有x2≥0; q:x=2是方程x+3=0的根,则下列命题为真命题的是( )
| A、¬p∧q | B、p∧¬q |
| C、¬p∧¬q | D、p∧q |
若角α满足α=
+
(k∈Z),则α的终边一定在( )
| 2kπ |
| 3 |
| π |
| 6 |
| A、第一象限或第二象限或第三象限 |
| B、第一象限或第二象限或第四象限 |
| C、第一象限或第二象限或x轴非负半轴上 |
| D、第一象限或第二象限或y轴非正半轴上 |
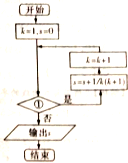
如图是求
+
+
+…+
的值的程序框图,则判断框①中应填( )
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |

| A、k≤99? |
| B、k<99? |
| C、k≤100? |
| D、k<98? |
圆x2+y2-2x+4y+1=0和圆x2+y2-6x+2y+9=0的位置关系是( )
| A、外离 | B、外切 | C、相交 | D、内切 |