题目内容
12.已知向量$\overrightarrow a$和$\overrightarrow b$的夹角为120°,且$|\overrightarrow a|=2,|\overrightarrow b|=1$.(1)求$(2\overrightarrow a-\overrightarrow b)•\overrightarrow a$的值;
(2)求$|\overrightarrow a+2\overrightarrow b|$的值.
分析 先求出$\overrightarrow{a}$•$\overrightarrow{b}$=-1,再根据向量的数量积即可求出
解答 解:(1)∵|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,向量$\overrightarrow a$和$\overrightarrow b$的夹角为120°
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2×1×cos120°=-1,
∴$(2\overrightarrow a-\overrightarrow b)•\overrightarrow a$=-$\overrightarrow{a}$•$\overrightarrow{b}$+2|$\overrightarrow{a}$|2=1+8=9,
(2)$|\overrightarrow a+2\overrightarrow b|$=4|$\overrightarrow{b}$|2+4$\overrightarrow{a}$•$\overrightarrow{b}$+|$\overrightarrow{a}$|2=4-4+4=4,
∴$|\overrightarrow a+2\overrightarrow b|$=2.
点评 本题考查了向量的数量积的运算和向量的模,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.有5本相同的数学书和3本相同的语文书,要将它们排在同一层书架上,并且语文书不能放在一起,则不同的放法数为( )
| A. | 20 | B. | 120 | C. | 2400 | D. | 14400 |
7.向边长为1的正方形内随机投一粒豆子,则豆子到正方形的顶点A的距离不大于$\frac{1}{2}$的概率是( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{π}$ | D. | $\frac{π}{16}$ |
17.五本不同的书在书架上排成一排,其中甲,乙两本必须连排,而丙,丁两本不能连排,则不同的排法共( )
| A. | 12种 | B. | 20种 | C. | 24种 | D. | 48种 |
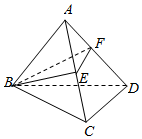 如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.
如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.