题目内容
7.如图,△ABC中,M是中线AD的中点.若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,∠BAC=60°,则$\overrightarrow{AM}$•$\overrightarrow{BM}$的值为-$\frac{9}{16}$.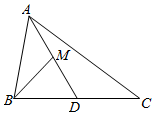
分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AM}$,$\overrightarrow{BM}$,再计算$\overrightarrow{AM}$•$\overrightarrow{BM}$.
解答 解:∵D是BC的中点,∴$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{AC}$-$\frac{1}{2}$$\overrightarrow{AB}$,
又M是AD的中点,∴$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$,$\overrightarrow{BM}$=$\frac{1}{2}$($\overrightarrow{BA}+\overrightarrow{BD}$)=$\frac{1}{4}$$\overrightarrow{AC}$-$\frac{3}{4}$$\overrightarrow{AB}$,
∴$\overrightarrow{AM}•\overrightarrow{BM}$=($\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$)•($\frac{1}{4}$$\overrightarrow{AC}$-$\frac{3}{4}$$\overrightarrow{AB}$)=-$\frac{3}{16}$${\overrightarrow{AB}}^{2}$+$\frac{1}{16}$$\overrightarrow{AC}$2-$\frac{1}{8}$$\overrightarrow{AB}•\overrightarrow{AC}$,
∵|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,∠BAC=60°,
∴${\overrightarrow{AB}}^{2}$=4,${\overrightarrow{AC}}^{2}$=9,$\overrightarrow{AB}•\overrightarrow{AC}$=2×3×cos60°=3,
∴$\overrightarrow{AM}•\overrightarrow{BM}$=-$\frac{3}{4}$+$\frac{9}{16}$-$\frac{3}{8}$=-$\frac{9}{16}$.
故答案为:-$\frac{9}{16}$.
点评 本题考查了平面向量的数量积运算,属于中档题.

| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
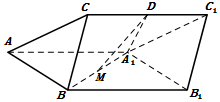 如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.