题目内容
函数y=xsinx+cosx的图象大致是( )
A、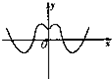 |
B、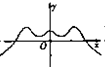 |
C、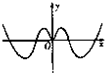 |
D、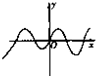 |
考点:函数的图象
专题:函数的性质及应用
分析:利用函数的奇偶性、单调性、特殊值,借助排除法能求出结果.
解答:
解:∵y=xsinx+cosx,
设f(x)=xsinx+cosx,
则f(-x)=(-x)sin(-x)+cos(-x)=xsinx+cosx=f(x),
∴y=xsinx+cosx是偶函数,故排除D.
当x=0时,y=0+cos0=1,故排除C和D;
∵y′=xcosx,
∴x>0开始时,函数是增函数,由此排除B.
故选:A.
设f(x)=xsinx+cosx,
则f(-x)=(-x)sin(-x)+cos(-x)=xsinx+cosx=f(x),
∴y=xsinx+cosx是偶函数,故排除D.
当x=0时,y=0+cos0=1,故排除C和D;
∵y′=xcosx,
∴x>0开始时,函数是增函数,由此排除B.
故选:A.
点评:本题考查函数的图象的性质的应用,是中档题,解题时要认真审题,注意排除法的合理运用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
设f(x)=
,则
f(x)dx=( )
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
已知复数z1=2-i,z2=1+i,则z1•z2在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设a∈R,函数f(x)=x3+ax2+(a-2)x为奇函数,在点(x0,f(x0))处的切线方程为y=x-2,则f(x0)=( )
| A、1 | B、-1 | C、1或-1 | D、-2 |
有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为( )
| A、5,11,17,23,29 |
| B、5,10,15,20,25 |
| C、5,15,20,35,40 |
| D、10,20,30,40,50 |
若0<x<3,则
+
的最小值为( )
| 1 |
| x |
| 2 |
| 3-x |
| A、2 | ||||
B、1+
| ||||
C、
| ||||
D、3+2
|