题目内容
已知tanα=-2，计算：
（1）
（2）
．
（1）
| 3sinα+2cosα |
| 5cosα-sinα |
（2）
| 3 |
| 2sinαcosα+cos2α |
考点：同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：利用同角三角函数间的基本关系，将所求关系式转化为关于tanα的式子，代入计算，可得结论．
解答：
解：（1）∵tanα=-2，
∴
=
=
=-
；
（2）
=
=
=
=-5．
∴
| 3sinα+2cosα |
| 5cosα-sinα |
| 3tanα+2 |
| 5-tanα |
| -6+2 |
| 5-(-2) |
| 4 |
| 7 |
（2）
| 3 |
| 2sinαcosα+cos2α |
| 3sin2α+3cos2α |
| 2sinαcosα+cos2α |
| 3tan2α+3 |
| 2tanα+1 |
| 3•4+3 |
| -3 |
点评：本题考查同角三角函数间的基本关系，将所求关系式转化为关于tanα的式子是关键，也是难点，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
直线过点（-3，4），且在两坐标轴上的截距之和为12，则直线方程为（ ）
| A、4x-y+16=0 |
| B、x+3y-9=0 |
| C、4x-y+16=0或x+3y-9=0 |
| D、2x+y-16=0 |
函数y=xsinx+cosx的图象大致是（ ）
A、 |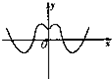
B、 |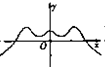
C、 |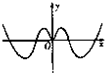
D、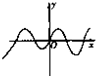 |