题目内容
设f(x)=
,则
f(x)dx=( )
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
考点:定积分
专题:导数的综合应用
分析:根据分段函数的积分性质即可得到结论.
解答:
解:∵f(x)=
,
∴
f(x)dx=
x2dx+
(2-x)dx=
x3
+(2x-
x2)
=
+(2×2-
×22)-2+
=
+2-2+
=
,
故选:A.
|
∴
| ∫ | 2 0 |
| ∫ | 1 0 |
| ∫ | 2 1 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 2 |
| | | 2 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
故选:A.
点评:本题主要考查分段函数的积分计算,要求熟练掌握常见函数的积分公式以及分段函数的积分性质.

练习册系列答案
相关题目
直线过点(-3,4),且在两坐标轴上的截距之和为12,则直线方程为( )
| A、4x-y+16=0 |
| B、x+3y-9=0 |
| C、4x-y+16=0或x+3y-9=0 |
| D、2x+y-16=0 |
已知等差数列{an}中,a5+a11=12,a4=2,则a12=( )
| A、5 | B、10 | C、15 | D、20 |
已知△ABC三条边为a,b,c,
=(a,cos
),
=(b,cos
),
=(c,cos
),且三个向量共线,则△ABC的形状是( )
| m |
| A |
| 2 |
| n |
| B |
| 2 |
| p |
| C |
| 2 |
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
函数f(x)=
(x∈R)的值域是( )
| 2 |
| 1+x2 |
| A、(0,2) |
| B、(0,2] |
| C、[0,2) |
| D、[0,2] |
函数y=xsinx+cosx的图象大致是( )
A、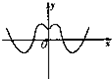 |
B、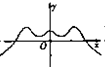 |
C、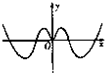 |
D、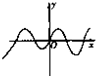 |