题目内容

若0＜x＜3，则
1
x
+
2
3-x
的最小值为（　　）
A、2
B、1+
2
2
3
C、
3
2
D、3+2
2
考点：基本不等式
专题：导数的综合应用
分析：令f（x）=
1
x
+
2
3-x
，（0＜x＜3），利用导数研究其单调性极值与最值即可得出．
解答： 解：令f（x）=
1
x
+
2
3-x
，（0＜x＜3），
则f′(x)=-
1
x2
+
2
(3-x)2
=
[x-(-3+3
2
)](x+3+3
2
)
x2(3-x)2
，
令f′（x）=0，由0＜x＜3，解得x=-3+3
2
．
当0＜x＜3
2
-3时，f′（x）＜0，函数单调递减；当3
2
-3＜x＜3时，f′（x）＞0，函数单调递增．
∴当x=3
2
-3时，函数f（x）取得极小值，即最小值，
且f(3
3
-3)=
1
3
2
-3
+
2
3-(3
2
-3)
=
2
+1
3
+
2+
2
3
=1+
2
2
3
．
故选：B．
点评：本题考查了导数研究其单调性极值与最值，属于基础题．
练习册系列答案
相关题目
某同学参加北大、清华、科大三所学校的自主命题招生考试，其被录取的概率分别为
1
5
，
1
4
，
1
3
（各学校是否录取他相互独立，允许他可以被多个学校同时录取）．则此同学至少被两所学校录取的概率为
 
．
函数f（x）=
2
1+x2
（x∈R）的值域是（　　）
A、（0，2）
B、（0，2]
C、[0，2）
D、[0，2]
函数y=xsinx+cosx的图象大致是（　　）
A、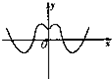
B、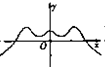
C、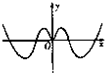
D、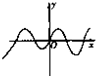
设一组数据的方差是S2，将这组数据的每个数都乘以10，所得到的一组新数据的方差是（　　）
A、0.1S2
B、S2
C、10S2
D、100S2
设a=sin（sin210°），b=sin（cos210°），c=cos（cos210°），d=cos（sin210°），则a、b、c、d中最大的是（　　）
A、aB、bC、cD、d
（1）求证f（x）=x3+x在（-∞，+∞）上是增函数；
（2）确定函数f(x)=
1
1-2x
的单调性．
已知函数f（x）=x2-1，设曲线y=f（x）在点（xn，yn）处的切线与x轴的交点为（xn+1，0），其中x1为正实数．
（1）用xn表示xn+1；
（2）x1=2，若an=lg
xn+1
xn-1
，试证明数列{an}为等比数列，并求数列{an}的通项公式；
（3）若数列{bn}的前n项和Sn=
n(n+1)
2
，记数列{an•bn}的前n项和Tn，求Tn．
已知f（x），g（x）都是定义在R上的函数，g（x）≠0，f′（x）g（x）＞f（x）g′（x），且f（x）=ax•g（x）（a＞0且a≠1），
f(1)
g(1)
+
f(-1)
g(-1)
=
5
2
．若数列{
f(n)
g(n)
}的前n项和大于62，则n的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网