题目内容
已知幂函数f（x）=xα在[1，2]上的最大值与最小值的和为5，则α= ．
考点：幂函数的性质
专题：计算题,函数的性质及应用
分析：根据幂函数在[1，2]上是单调函数，进而可得其最大最小值，相加可得答案．
解答：
解：函数幂函数f（x）=xα在[1，2]上是单调函数，
∴最大值和最小值在区间端点取得，
它们之和为5，即1α+2α=5，解得α=2．
故答案为：2．
∴最大值和最小值在区间端点取得，
它们之和为5，即1α+2α=5，解得α=2．
故答案为：2．
点评：本题考查幂函数的单调性的应用，难度不大．
练习册系列答案
备战中考寒假系列答案
相关题目
直线过点（-3，4），且在两坐标轴上的截距之和为12，则直线方程为（ ）
| A、4x-y+16=0 |
| B、x+3y-9=0 |
| C、4x-y+16=0或x+3y-9=0 |
| D、2x+y-16=0 |
函数y=xsinx+cosx的图象大致是（ ）
A、 |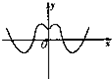
B、 |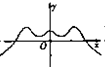
C、 |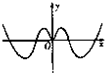
D、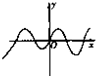 |