题目内容
设a∈R,函数f(x)=x3+ax2+(a-2)x为奇函数,在点(x0,f(x0))处的切线方程为y=x-2,则f(x0)=( )
| A、1 | B、-1 | C、1或-1 | D、-2 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:由函数是奇函数求得a的值,代入原函数后求导,由导函数等于1求得点(x0,f(x0))的横坐标,进一步求得f(x0)的值.
解答:
解:∵函数f(x)=x3+ax2+(a-2)x为奇函数,
f(-1)=(-1)3+a•(-1)2+(a-2)•(-1)=1,
-f(1)=-2a+1,
∴f(-1)=-f(1),即-2a+1=1,a=0.
∴f(x)=x3-2x,
f′(x0)=3x02-2,
∵函数在点(x0,f(x0))处的切线方程为y=x-2,
∴3x02-2=1,解得x0=±1.
当x0=1时,f(x0)=-1,
当x0=-1时,f(x0)=1.
故选:C.
f(-1)=(-1)3+a•(-1)2+(a-2)•(-1)=1,
-f(1)=-2a+1,
∴f(-1)=-f(1),即-2a+1=1,a=0.
∴f(x)=x3-2x,
f′(x0)=3x02-2,
∵函数在点(x0,f(x0))处的切线方程为y=x-2,
∴3x02-2=1,解得x0=±1.
当x0=1时,f(x0)=-1,
当x0=-1时,f(x0)=1.
故选:C.
点评:本题考查了利用导数研究曲线上某点处的切线方程,函数在某点处的导数值就是对应曲线上该点处的切线的斜率,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等差数列{an}中,a5+a11=12,a4=2,则a12=( )
| A、5 | B、10 | C、15 | D、20 |
函数f(x)=
(x∈R)的值域是( )
| 2 |
| 1+x2 |
| A、(0,2) |
| B、(0,2] |
| C、[0,2) |
| D、[0,2] |
某人从湖中打了一网鱼,共有m条,做上记号再放入湖中,数日后在此湖中又打了一网鱼,共有n条,其中k条有记号,则估计湖中有鱼( )
A、
| ||
B、m•
| ||
C、m•k•
| ||
| D、无法估计 |
函数y=xsinx+cosx的图象大致是( )
A、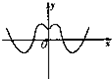 |
B、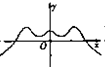 |
C、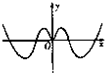 |
D、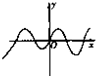 |
设一组数据的方差是S2,将这组数据的每个数都乘以10,所得到的一组新数据的方差是( )
| A、0.1S2 |
| B、S2 |
| C、10S2 |
| D、100S2 |