题目内容
已知数列{an}的前n项和为Sn=rn-1(r>0,r≠1),且
=27.
(1)求r的值及数列{an}的通项公式;
(2)设bn=an2,求数列{bn}的前n项和Tn.
| a5 |
| a2 |
(1)求r的值及数列{an}的通项公式;
(2)设bn=an2,求数列{bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由题意化简a2=S2-S1、a5=S5-S4,代入
=27化简求出r的值,利用an=
和等比数列的通项公式求出an;
(2)由(1)条件化简bn=an2,利用等比数列的前n项和公式求出Tn.
| a5 |
| a2 |
|
(2)由(1)条件化简bn=an2,利用等比数列的前n项和公式求出Tn.
解答:
解:(1)由题意知,Sn=rn-1(r>0,r≠1),
则a2=S2-S1=(r2-1)-(r-1)=r2-r,
a5=S5-S4=(r5-1)-(r4-1)=r5-r4,
因为
=27,所以
=27,解得r=3,
则Sn=3n-1,
当n=1时,a1=S1=3-1=2,
当n≥2时,an=Sn-Sn-1=3n-1-(3n-1-1)=2•3n-1,
当n=1时,也适合上式,所以an=2•3n-1;
(2)由(1)得,bn=an2=4•32n-2=4•9n-1,
所以Tn=4(9+92+93+…+9n-1)=4×
=
,
则Tn=
.
则a2=S2-S1=(r2-1)-(r-1)=r2-r,
a5=S5-S4=(r5-1)-(r4-1)=r5-r4,
因为
| a5 |
| a2 |
| r5-r4 |
| r2-r |
则Sn=3n-1,
当n=1时,a1=S1=3-1=2,
当n≥2时,an=Sn-Sn-1=3n-1-(3n-1-1)=2•3n-1,
当n=1时,也适合上式,所以an=2•3n-1;
(2)由(1)得,bn=an2=4•32n-2=4•9n-1,
所以Tn=4(9+92+93+…+9n-1)=4×
| 9(1-9n) |
| 1-9 |
| 9(9n-1) |
| 2 |
则Tn=
| 9(9n-1) |
| 2 |
点评:本题考查等比数列的通项公式、前n项和公式,以及公式an=
的应用,考查方程思想和化简能力.
|

练习册系列答案
相关题目
已知向量
=(1,2),
=(2x,-3),若
⊥(
+
),则x=( )
| a |
| b |
| a |
| a |
| b |
| A、3 | ||
B、-
| ||
| C、-3 | ||
D、
|
设x是a与b的等差中项,x2是a2与-b2的等差中项,则a,b的关系是( )
| A、a=-b |
| B、a=3b |
| C、a=-b或a=3b |
| D、a=b=0 |
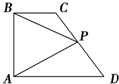 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则