题目内容
用数学归纳法证明:(1+
)(1+
)…(1+
)>
(n≥2)
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| ||
| 2 |
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:直接利用数学归纳法的证明步骤证明不等式,(1)验证n=2时不等式成立;(2)假设当n=k(k≥1)时成立,利用放缩法证明n=k+1时,不等式也成立.
解答:
证明:(1)当n=2时,左边=1+
=
>
,∴n=2时成立;
(2)假设当n=k(k≥1)时成立,即:(1+
)(1+
)…(1+
)>
那么当n=k+1时,左边=(1+
)(1+
)…(1+
)(1+
)>
•(1+
)=
,
∵
<2k+2,
∴
>
,
∴n=k+1时也成立
根据(1)(2)可得不等式对所有的n≥2都成立.
| 1 |
| 3 |
| 4 |
| 3 |
| ||
| 2 |
(2)假设当n=k(k≥1)时成立,即:(1+
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2k-1 |
| ||
| 2 |
那么当n=k+1时,左边=(1+
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2k-1 |
| 1 |
| 2k+1 |
| ||
| 2 |
| 1 |
| 2k+1 |
| 2k+2 | ||
2
|
∵
| (2k+1)(2k+3) |
∴
| 2k+2 | ||
2
|
| ||
| 2 |
∴n=k+1时也成立
根据(1)(2)可得不等式对所有的n≥2都成立.
点评:本题是中档题,考查数学归纳法的证明步骤,注意不等式的证明方法,放缩法的应用,考查逻辑推理能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设
,
是单位向量,则“
•
>0”是“
和
的夹角为锐角”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
中小学校车安全引起社会的关注,为了彻底消除校车安全隐患,某市购进了50台完全相同的校车,准备发放给10所学校,每所学校至少2台,则不同的发放方案种数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知g(x)=ax+1,f(x)=
,对?x1∈[-2,2],?x2∈[-2,2].,使g(x1)=f(x2)成立,则a的取值范围是( )
|
| A、[-1,+∞) |
| B、[-1,1] |
| C、(0,1] |
| D、(-∞,1] |
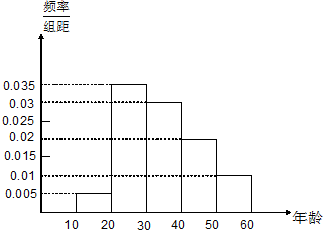 某班同学利用寒假进行社会实践,对年龄段在[10,60]的人生活习惯是否符合环保理念进行调查,现随机抽取n人进行数据分析,得到如下频率分布表和频率分布直方图;
某班同学利用寒假进行社会实践,对年龄段在[10,60]的人生活习惯是否符合环保理念进行调查,现随机抽取n人进行数据分析,得到如下频率分布表和频率分布直方图;