题目内容
求函数f（x）=9x+3x+1+1的值域．
考点：指数型复合函数的性质及应用
专题：函数的性质及应用
分析：令t=3x＞0，可得函数f（x）=g（t）=t2+3t+1=(t+
)2-
，再利用二次函数的性质求得它的值域．
| 3 |
| 2 |
| 5 |
| 4 |
解答：
解：令t=3x＞0，可得函数f（x）=9x+3x+1+1=g（t）=t2+3t+1=(t+
)2-
，
故g（t）＞g（0）=1，故函数的值域为（1，+∞）．
| 3 |
| 2 |
| 5 |
| 4 |
故g（t）＞g（0）=1，故函数的值域为（1，+∞）．
点评：本题主要考查指数函数的值域，二次函数的性质，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=3-2|x|，g（x）=x2，构造函数F（x）=
，那么函数y=F（x）（ ）
|
| A、有最大值1，最小值-1 |
| B、有最小值-1，无最大值 |
| C、有最大值1，无最小值 |
| D、有最大值3，最小值1 |
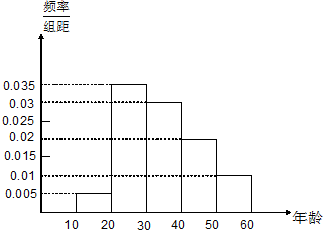某班同学利用寒假进行社会实践，对年龄段在[10，60]的人生活习惯是否符合环保理念进行调查，现随机抽取n人进行数据分析，得到如下频率分布表和频率分布直方图；已知g（x）=ax+1，f（x）=
，对?x1∈[-2，2]，?x2∈[-2，2]．，使g（x1）=f（x2）成立，则a的取值范围是（ ）
|
| A、[-1，+∞） |
| B、[-1，1] |
| C、（0，1] |
| D、（-∞，1] |