题目内容
已知平面向量
=
,
=
,|
|=4,|
|=3,∠BAC=β,(2
-3
)•(2
+
)=61
(1)求β的大小;
(2)求|
|.
| AB |
| a |
| AC |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
(1)求β的大小;
(2)求|
| BC |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:(1)运用向量的平方即为模的平方,结合向量的夹角公式,计算即可得到夹角;
(2)运用向量的三角形法则和向量的平方即为模的平方,计算即可得到.
(2)运用向量的三角形法则和向量的平方即为模的平方,计算即可得到.
解答:
解:(1)由于(2
-3
)•(2
+
)=61,
展开得4
2-4
•
-3
2=61,
由于|
|=4,|
|=3,则4×16-4
•
-3×9=61,
•
=-6,
cosβ=
=
=-
由0≤β≤π,则β=
;
(2)|
|=|
-
|=
=
=
=
=
.
| a |
| b |
| a |
| b |
展开得4
| a |
| a |
| b |
| b |
由于|
| a |
| b |
| a |
| b |
| a |
| b |
cosβ=
| ||||
|
|
| -6 |
| 4×3 |
| 1 |
| 2 |
由0≤β≤π,则β=
| 2π |
| 3 |
(2)|
| BC |
| AC |
| AB |
(
|
|
=
42-2•4•3cos
|
| 16+12+9 |
=
| 37 |
点评:本题考查向量的数量积的夹角公式和向量的性质:向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=3-2|x|,g(x)=x2,构造函数F(x)=
,那么函数y=F(x)( )
|
| A、有最大值1,最小值-1 |
| B、有最小值-1,无最大值 |
| C、有最大值1,无最小值 |
| D、有最大值3,最小值1 |
设
,
是单位向量,则“
•
>0”是“
和
的夹角为锐角”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
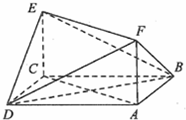 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=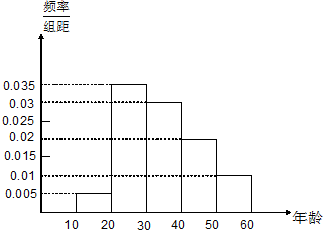 某班同学利用寒假进行社会实践,对年龄段在[10,60]的人生活习惯是否符合环保理念进行调查,现随机抽取n人进行数据分析,得到如下频率分布表和频率分布直方图;
某班同学利用寒假进行社会实践,对年龄段在[10,60]的人生活习惯是否符合环保理念进行调查,现随机抽取n人进行数据分析,得到如下频率分布表和频率分布直方图;