题目内容

直线y=
2
π
x与曲线y=sinx围成的区域面积为
 
．
考点：定积分
专题：导数的概念及应用
分析：分别画出直线y=
2
π
x与曲线y=sinx的图象，确定出交点，积分区间，则问题可解．
解答： 解：分别画出直线y=
2
π
x与曲线y=sinx，如图所示，
则y=
2
π
x与曲线y=sinx的交点坐标是（-
π
2
，0），（0，0），（
π
2
，0），
∴直线y=
2
π
x与曲线y=sinx围成的区域面积S=2
∫
π
2
0
（sinx-
2
π
x）dx=2（-cosx-
1
π
x2）|
 
π
2
0
=2[（0-
π
4
）+1]|=2-
π
2
，
故答案为：2-
π
2
．
点评：本题考查了定积分的几何意义及其求法，属于基础题．
练习册系列答案
相关题目
设A（1，2），B（3，-1），C（3，4），则
AB
•
AC
（　　）
A、11B、5C、-2D、1
已知向量
a
=（x2+1，p+2），
b
=（3，x），f（x）=
a
•
b
，p是实数．
（1）若存在唯一实数x，使
a
+
b
与
c
=（1，2）平行，试求p的值；
（2）若函数y=f（x）是偶函数，试求函数y=|f（x）-15|在区间[-1，3]上的值域；
（3）若函数f（x）在区间[-
1
2
，+∞）上是增函数，试讨论方程f（x）+
x
-p=0解的个数，说明理由．
已知数列{an}的前n项和为Sn=rn-1（r＞0，r≠1），且
a5
a2
=27．
（1）求r的值及数列{an}的通项公式；
（2）设bn=an2，求数列{bn}的前n项和Tn．
极坐标方程ρ=
2
1+cosθ
化为普通方程是（　　）
A、y2=4（x-1）
B、y2=4（1-x）
C、y2=2（x-1）
D、y2=2（1-x）
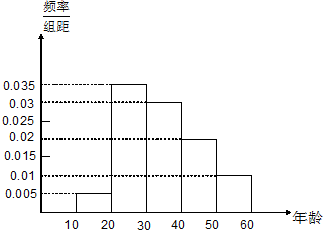某班同学利用寒假进行社会实践，对年龄段在[10，60]的人生活习惯是否符合环保理念进行调查，现随机抽取n人进行数据分析，得到如下频率分布表和频率分布直方图；
（1）求出频率分布表中n，x，y的值；
（2）现从第三、四、五组中，采用分层抽样法抽取12人参加户外环保体验活动，则从这三组中应各抽取多少人？
（3）从第三、四、五组中采用分层抽样法抽取12人参加项学习活动，从这12名中再选取3人作为领队，记这3名领队中在第三四组内人数为X，求X分布列和期望EX．
组数分组人数频率
第一组[10，20）5 
第二组[20，30） x
第三组[30，40）  
第四组[40，50）y 
第五组[50，60] 
合计 n
7名同学中，有5名会下象棋，有4名会下围棋，现从7人中选2人分别参加象棋和围棋比赛，共有多少种不同的选法？
已知数列{an}的通项公式an=a•（
1
2
）n（a≠0），试判断数列的增减性．
若将函数y=sin2x的图象向左平移φ，φ∈（0，
π
2
）个单位，再向下平移一个单位所得的函数图象过点P（
π
3
，-
1
2
），则φ的取值为（　　）
A、
π
24
B、
π
12
C、
π
6
D、
π
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网