题目内容
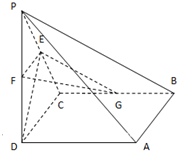 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F分别为PC、PD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F分别为PC、PD的中点.(1)求证:DE⊥平面PBC
(2)在棱BC上确定一点G,使得PA∥面EFG,并写出证明过程
(3)在(2)成立的条件下,求二面角F-EG-C的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得DE⊥PC,PD⊥BC,BC⊥CD,从而BC⊥平面PCD,由此能证明DE⊥平面PBC.
(2)棱BC中点G使得PA∥面EFG.以DA,DC,DP为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能证明PA∥面EFG.
(Ⅲ)由面EGC的法向量为
=(0,1,1),利用向量法能求出二面角F-EG-C的余弦值.
(2)棱BC中点G使得PA∥面EFG.以DA,DC,DP为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能证明PA∥面EFG.
(Ⅲ)由面EGC的法向量为
| n |
解答:
(1)证明:∵底面ABCD为正方形,PD=AB=2,E为PC的中点,∴DE⊥PC.
∵PD⊥平面ABCD,BC?平面ABCD,∴PD⊥BC.
∵ABCD为正方形,∴BC⊥CD,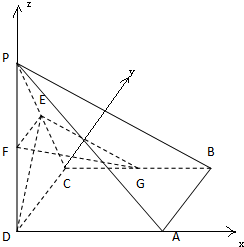
∵PD∩DC=D,∴BC⊥平面PCD,
∵DE?平面PCD,∴BC⊥DE,
∴DE⊥平面PBC.…(4分)
(2)解:棱BC中点G使得PA∥面EFG.
证明如下:以DA,DC,DP为x轴,y轴,z轴,
建立空间直角坐标系,
则D(0,0,0),A(2,0,0),P(0,0,2),
E(0,1,1),F(0,0,1),B(2,2,0),
C(0,2,0),
设G(x,y,z)设
=λ
,则(x,y-2,z)=λ(1,0,0)∴G(λ,2,0).
面EFG的法向量为
=(1,0,1),
=(2,0,-2),
∵
•
=0,∴PA∥面EFG.…(8分)
(Ⅲ)设面EGC的法向量为
=(0,1,1),
∴cosθ=
,∵二面角F-EG-C的平面角为钝角,
∴二面角F-EG-C的余弦值为-
.…(12分)
∵PD⊥平面ABCD,BC?平面ABCD,∴PD⊥BC.
∵ABCD为正方形,∴BC⊥CD,

∵PD∩DC=D,∴BC⊥平面PCD,
∵DE?平面PCD,∴BC⊥DE,
∴DE⊥平面PBC.…(4分)
(2)解:棱BC中点G使得PA∥面EFG.
证明如下:以DA,DC,DP为x轴,y轴,z轴,
建立空间直角坐标系,
则D(0,0,0),A(2,0,0),P(0,0,2),
E(0,1,1),F(0,0,1),B(2,2,0),
C(0,2,0),
设G(x,y,z)设
| CG |
| CB |
面EFG的法向量为
| m |
| PA |
∵
| PA |
| m |
(Ⅲ)设面EGC的法向量为
| n |
∴cosθ=
| 1 |
| 2 |
∴二面角F-EG-C的余弦值为-
| 1 |
| 2 |
点评:本题考查直线与平面垂直的证明,考查棱BC上确定一点G,使得PA∥面EFG,并写出证明过程,考查二面角F-EG-C的余弦值的求法,解题时要注意向量法的合理运用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知复数
=1-i,则复数z的共轭复数
等于( )
| 2 |
| z |
. |
| z |
| A、-2i | B、2i |
| C、1-i | D、1+i |
过已知点A(2,3),B(1,5)的直线AB的斜率是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
cos70°•cos20°-sn70°•sin20°的值是( )
| A、0 | B、1 |
| C、sin50° | D、cos50° |