题目内容
已知集合A={x|(x-2)(x-3a-1)<0},y=lg
的定义域为集合B.
(1)若A=B,求实数a;
(2)是否存在实数a使得A∩B=ϕ,若存在,则求出实数a的值,若不存在,说明理由.
| 2a-x |
| x-(a2+1) |
(1)若A=B,求实数a;
(2)是否存在实数a使得A∩B=ϕ,若存在,则求出实数a的值,若不存在,说明理由.
考点:函数的定义域及其求法,交集及其运算
专题:函数的性质及应用,集合
分析:(1)由集合B非空得出a≠1,对3a+1与2的大小比较,可分①当a>
且a≠1时,②当a=
时,③当a<
时3种情况,利用A=B求得a的值;
(2)仍分第(1)问的三种情况,化简集合A,再由条件A∩B=φ求得a的范围.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)仍分第(1)问的三种情况,化简集合A,再由条件A∩B=φ求得a的范围.
解答:
解:(1)由于函数的定义域是非空数集,故a≠1.
①当a>
且a≠1时,A=(2,3a+1),B=(2a,a2+1),由A=B可得:
,
方程组无解;
②当a=
时,A=φ,A=B不可能;
③当a<
时,A=(3a+1,2),B=(2a,a2+1),由A=B可得:
,
∴a=-1.
(2)①当a>
且a≠1时,A=(2,3a+1),B=(2a,a2+1),由A∩B=φ可得3a+1≤2a或a2+1≤2,
又a>
且a≠1,则
<a<1;
②当a=
时,A=φ,则A∩B=φ,符合题意;
③当a<
时,A=(3a+1,2),B=(2a,a2+1),由A∩B=φ可得2≤2a或a2+1≤3a+1,
又a<
,则0≤a<
.
∴当a∈[0,1)时,A∩B=φ..
①当a>
| 1 |
| 3 |
|
方程组无解;
②当a=
| 1 |
| 3 |
③当a<
| 1 |
| 3 |
|
∴a=-1.
(2)①当a>
| 1 |
| 3 |
又a>
| 1 |
| 3 |
| 1 |
| 3 |
②当a=
| 1 |
| 3 |
③当a<
| 1 |
| 3 |
又a<
| 1 |
| 3 |
| 1 |
| 3 |
∴当a∈[0,1)时,A∩B=φ..
点评:本题主要考查函数的定义域的求法,同时考查集合与集合之间的关系,对于含有字母的函数定义域的求法,通常要讨论.

练习册系列答案
相关题目
若变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、5 | B、4 | C、3 | D、2 |
如图是一个算法的程序框图,则输出的结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
甲、乙两人在一次赛跑中路程s与t的函数关系如图所示,则下列说法正确的是( )
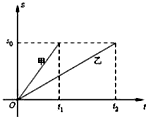

| A、甲比乙先出去 |
| B、乙比甲跑的路程多 |
| C、甲先到达终点 |
| D、甲、乙两人的速度相同 |
已知方程x2+x+m=0(m∈R)有两个虚根α,β,若|α-β|=3,则m的值是( )
A、-2或
| ||
| B、-2 | ||
C、
| ||
D、-
|