题目内容
已知方程x2+x+m=0(m∈R)有两个虚根α,β,若|α-β|=3,则m的值是( )
A、-2或
| ||
| B、-2 | ||
C、
| ||
D、-
|
考点:复数求模
专题:数系的扩充和复数
分析:利用根与系数的关系即可得出.
解答:
解:∵方程x2+x+m=0(m∈R)有两个虚根α,β,
∴α+β=-1,αβ=m.
∵|α-β|=3,
∴
=3,
∴
=3,解得m=-2.
故选:B.
∴α+β=-1,αβ=m.
∵|α-β|=3,
∴
| (α+β)2-4αβ |
∴
| 1-4m |
故选:B.
点评:本题考查了实系数一元二次方程有虚根时利用根与系数的关系的方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
执行如图所示的程序,则输出结果S的值为( )


| A、6 | B、14 | C、10 | D、30 |
已知命题P:?x∈(0,
),使得cosx≤x,则该命题是否定为( )
| π |
| 2 |
A、?x∈(0,
| ||
B、?x∈(0,
| ||
C、?x∈(0,
| ||
D、?x∈(0,
|
直线l过点A(3,1)与x轴正向、y轴正向分别交于M、N两点,则|MA|•|NA|的最小值为( )
| A、2 | B、4 | C、6 | D、8 |
下列命题是真命题的是( )
| A、-1的平方根只有一个 |
| B、i是1的四次方根 |
| C、i是-1的立方根 |
| D、i是方程x2-1的根 |
在正方体ABCD-A1B1C1D1中,下列四队截面中彼此平行的一对是( )
| A、A1BC1与ACD1 |
| B、B1CD1与BDC1 |
| C、B1D1D与BDA1 |
| D、A1DC1与AD1C |
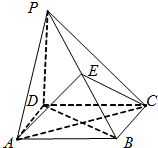 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BAD=60°,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BAD=60°,PD⊥底面ABCD,点E在棱PB上.