题目内容
已知命题“如果x⊥y，y∥z，则x⊥z”是假命题，那么字母x，y，z在空间所表示的几何图形可能是（ ）
| A、全是直线 |
| B、全是平面 |
| C、x，z是直线，y是平面 |
| D、x，y是平面，z是直线 |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：对四个选项中的命题分别依据线面的位置关系判断，找出不成立的即为正确选项
解答：
解：对于A，一条直线垂直于两条平行线中的一条，也必垂直于另一条，故不满足命题是假命题；
对于B，一个平面垂直于两个平行平面中的一个，也必垂直于另一个，故不满足命题是假命题；
对于C．一条直线垂直于一个平面，必垂直于与这个平面平行的直线，故不满足命题是假命题；
对于D，两个平面垂直，则它与另一个平面的位置关系可能是平行，相交，或在另一面内，故此命题是假命题．
故选：D．
对于B，一个平面垂直于两个平行平面中的一个，也必垂直于另一个，故不满足命题是假命题；
对于C．一条直线垂直于一个平面，必垂直于与这个平面平行的直线，故不满足命题是假命题；
对于D，两个平面垂直，则它与另一个平面的位置关系可能是平行，相交，或在另一面内，故此命题是假命题．
故选：D．
点评：本题以立体几何中线面位置关系为题面考查了命题真假的判断，熟练掌握空间中点线面的位置关系是解答的关键
练习册系列答案
相关题目
已知非零向量
，
，则“
-2
=
”是“|
+
|=|
|+|
|”成立的（ ）
| a |
| b |
| a |
| b |
| 0 |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
命题p：
≤0；命题q：y=xa（x为自变量）在第一象限是增函数，则p是q的（ ）
| a |
| a-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某校高二年级文科共303名学生，为了调查情况，学校决定随机抽取50人参加抽测，采取先简单随机抽样去掉3人然后系统抽样抽取出50人的方式进行．则在此抽样方式下，某学生甲被抽中的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
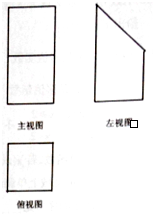某几何体的三视图如图所示，俯视图是边长为1的正方形，主视图上下都是边长为1的正方形，则该几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
| D、2 |