题目内容
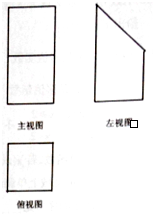某几何体的三视图如图所示，俯视图是边长为1的正方形，主视图上下都是边长为1的正方形，则该几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是直四棱柱，根据三视图判断其侧棱长和底面四边形的形状及相关几何量的数据，把数据代入棱柱的体积公式计算．
解答：
解：由三视图知：几何体是直四棱柱，
其中侧棱长为1，底面是直角梯形，直角梯形的直角腰长为1，两底边长分别为1和2，
∴几何体的体积V=
×1×1=
．
故选：C．
其中侧棱长为1，底面是直角梯形，直角梯形的直角腰长为1，两底边长分别为1和2，
∴几何体的体积V=
| 1+2 |
| 2 |
| 3 |
| 2 |
故选：C．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．
练习册系列答案
寒假学与练系列答案
相关题目
若变量x，y满足约束条件
，则x+2y的最大值为（ ）
|
A、
| ||
B、
| ||
| C、3 | ||
D、2
|
复数z=
在复平面上对应的点所在的象限是（ ）
| 1-i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数f（x）=（ex+e-x）sinx的部分图象大致为（ ）
A、 |
B、 |
C、 |
D、 |
已知集合A={x|3≤x≤8}，B={x|x2-8x+12＜0}，则A∩B=（ ）
| A、{x|2＜x≤8} |
| B、{x|2＜x≤6} |
| C、{x|3≤x＜6} |
| D、{x|6＜x≤8} |
已知命题“如果x⊥y，y∥z，则x⊥z”是假命题，那么字母x，y，z在空间所表示的几何图形可能是（ ）
| A、全是直线 |
| B、全是平面 |
| C、x，z是直线，y是平面 |
| D、x，y是平面，z是直线 |
已知M={x|x=2m-1，m∈Z}，N={x|x2-x-12＜0，x∈R}，则集合M∩N等于（ ）
| A、{-3，-1，1，3} |
| B、{1，3} |
| C、{0，1，2，3} |
| D、{-1，1，3} |