题目内容
已知双曲线
-
=1(b∈N*)的两个焦点为F1,F2,O为坐标原点,点P在双曲线上,且|OP|<5,若|PF1|、|F1F2|、|PF1|成等比数列,则b2等于( )
| x2 |
| 4 |
| y2 |
| b2 |
| A、1 | B、2 | C、3 | D、4 |
考点:双曲线的简单性质,等比数列的通项公式
专题:综合题,圆锥曲线的定义、性质与方程
分析:通过等比数列双曲线的定义,余弦定理推出:|OP|2=20+3b2.利用|OP|<5,b∈N,求出b的值
解答:
解:由题意,|PF1|、|F1F2|、|PF2|成等比数列可知,|F1F2|2=|PF1||PF2|,
即4c2=|PF1||PF2|,
由双曲线的定义可知|PF1|-|PF2|=4,即|PF1|2+|PF2|2-2|PF1||PF2|=16,
可得|PF1|2+|PF2|2-8c2=16…①
设∠POF1=θ,则∠POF2=π-θ,
由余弦定理可得:|PF2|2=c2+|OP|2-2|OF2||OP|cos(π-θ),|PF1|2=c2+|OP|2-2|OF1||OP|cosθ,
|PF2|2+PF1|2=2c2+2|OP|2,…②,
由①②化简得:|OP|2=8+3c2=20+3b2.
因为|OP|<5,b∈N,所以20+3b2<25.
所以b=1.
故选:A
即4c2=|PF1||PF2|,
由双曲线的定义可知|PF1|-|PF2|=4,即|PF1|2+|PF2|2-2|PF1||PF2|=16,
可得|PF1|2+|PF2|2-8c2=16…①
设∠POF1=θ,则∠POF2=π-θ,
由余弦定理可得:|PF2|2=c2+|OP|2-2|OF2||OP|cos(π-θ),|PF1|2=c2+|OP|2-2|OF1||OP|cosθ,
|PF2|2+PF1|2=2c2+2|OP|2,…②,
由①②化简得:|OP|2=8+3c2=20+3b2.
因为|OP|<5,b∈N,所以20+3b2<25.
所以b=1.
故选:A
点评:本题考查双曲线的定义,余弦定理以及等比数列的应用,是有难度的综合问题,考查分析问题解决问题的能力

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
某几何体的三视图如图所示,根据图中标出的数据,可得这个几何体的体积为( )
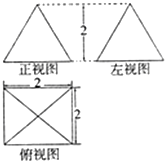

A、4+4
| ||
B、4+4
| ||
C、
| ||
| D、12 |
有一抛物线型拱桥,当水面离拱顶2米时,水面宽4米,则当水面下降1米后,水面宽度为( )
| A、9 | ||
| B、4.5 | ||
C、
| ||
D、2
|
已知
,
,
是空间的一个基底,设
=
+
,
=
-
,则下列向量中可以与
,
一起构成空间的另一个基底的是( )
| a |
| b |
| c |
| p |
| a |
| b |
| q |
| a |
| b |
| p |
| q |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
已知点P,A,B在双曲线
-
=1上,直线AB过坐标原点,且直线PA、PB的斜率之积为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|