题目内容
已知直线l过点(-1,0),l与圆C:(x-1)2+y2=3相交于A、B两点,则弦长|AB|≥2的概率为 .
考点:几何概型
专题:概率与统计
分析:先找出使弦长|AB|=2时的情况,再求直线与圆相切时的情形,根据几何概型的概率公式求解即可.
解答:
解:圆点是(1,0)半径是
,
可知(-1,0)在圆外 要使得弦长|AB|≥2 由半径是
,
设过圆点垂直于AB的直线 垂足为C 可得出圆点到AB的距离是
,
再由(-1,0)(1,0)和C点构成的直角三角形中 可知过(-1,0)的直线与x轴成45°
当直线与圆相切时,过(-1,0)的直线与x轴成60°
所以概率为:
=
.
故答案为:
.
| 3 |
可知(-1,0)在圆外 要使得弦长|AB|≥2 由半径是
| 3 |
设过圆点垂直于AB的直线 垂足为C 可得出圆点到AB的距离是
| 2 |
再由(-1,0)(1,0)和C点构成的直角三角形中 可知过(-1,0)的直线与x轴成45°
当直线与圆相切时,过(-1,0)的直线与x轴成60°
所以概率为:
| 45°+45° |
| 60°+60° |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题主要考查集合概型,属于基础题.

练习册系列答案
相关题目
已知双曲线
-
=1(b∈N*)的两个焦点为F1,F2,O为坐标原点,点P在双曲线上,且|OP|<5,若|PF1|、|F1F2|、|PF1|成等比数列,则b2等于( )
| x2 |
| 4 |
| y2 |
| b2 |
| A、1 | B、2 | C、3 | D、4 |
设x,y满足约束条件
且,z=x+ay的最小值为17,则a=( )
|
| A、-7 | B、5 |
| C、-7或5 | D、-5或7 |
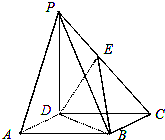 如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.
如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.