题目内容
有一抛物线型拱桥,当水面离拱顶2米时,水面宽4米,则当水面下降1米后,水面宽度为( )
| A、9 | ||
| B、4.5 | ||
C、
| ||
D、2
|
考点:抛物线的应用
专题:圆锥曲线的定义、性质与方程
分析:先建立直角坐标系,将A点代入抛物线方程求得m,得到抛物线方程,再把y=-3代入抛物线方程求得x0进而得到答案.
解答:
 解:如图建立直角坐标系,设抛物线方程为x2=my,
解:如图建立直角坐标系,设抛物线方程为x2=my,
将A(2,-2)代入x2=my,
得m=-2
∴x2=-2y,代入B(x0,-3)得x0=
,
故水面宽为2
m.
故选:D.
 解:如图建立直角坐标系,设抛物线方程为x2=my,
解:如图建立直角坐标系,设抛物线方程为x2=my,将A(2,-2)代入x2=my,
得m=-2
∴x2=-2y,代入B(x0,-3)得x0=
| 6 |
故水面宽为2
| 6 |
故选:D.
点评:本题主要考查抛物线的应用.考查了学生利用抛物线解决实际问题的能力.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
集合P={(x,y)|(x-2cosθ)2+(y-2sinθ)2=1,0≤θ≤2π},集合Q={(x,y)|y≥
x},若P⊆Q,则θ的取值范围是( )
| ||
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
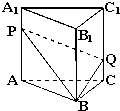 如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )
如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )| A、2:1 | B、3:1 |
| C、3:2 | D、4:3 |
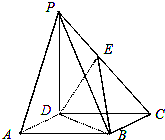 如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.
如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.