题目内容
过三点A（-4，0），B（0，2）和原点O（0，0）的圆的标准方程为 ．
考点：圆的标准方程
专题：直线与圆
分析：由条件利用圆的弦的性质求出圆心的坐标，可得圆的半径，从而求得圆的标准方程．
解答：
解：由于所求的圆经过三点A（-4，0），B（0，2）和原点O（0，0），
故圆心在直线x=-2上，又在y=1上，故圆心的坐标为M（-2，1），
半径为MO=
，故要求的圆的标准方程为（x+2）2+（y-1）2=5，
故答案：（x+2）2+（y-1）2=5．
故圆心在直线x=-2上，又在y=1上，故圆心的坐标为M（-2，1），
半径为MO=
| 5 |
故答案：（x+2）2+（y-1）2=5．
点评：本题主要考查求圆的标准方程，关键在于利用圆的弦的性质求出圆心的坐标，属于基础题．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、0∈N* | ||
B、
| ||
| C、0∈∅ | ||
| D、-2∈Z |
集合P={（x，y）|（x-2cosθ）2+（y-2sinθ）2=1，0≤θ≤2π}，集合Q={（x，y）|y≥
x}，若P⊆Q，则θ的取值范围是（ ）
| ||
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
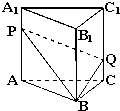如图，已知直三棱柱ABC-A1B1C1，点P、Q分别在棱AA1和CC1上，AP=C1Q，则平面BPQ把三棱柱分成两部分的体积比为（ ）| A、2：1 | B、3：1 |
| C、3：2 | D、4：3 |
已知直线ax+2y+2=0与直线3x-y-2=0平行，则a的值为（ ）
| A、-6 | B、6 | C、-3 | D、3 |
已知双曲线
-
=1（b∈N*）的两个焦点为F1，F2，O为坐标原点，点P在双曲线上，且|OP|＜5，若|PF1|、|F1F2|、|PF1|成等比数列，则b2等于（ ）
| x2 |
| 4 |
| y2 |
| b2 |
| A、1 | B、2 | C、3 | D、4 |
设x，y满足约束条件
且，z=x+ay的最小值为17，则a=（ ）
|
| A、-7 | B、5 |
| C、-7或5 | D、-5或7 |