题目内容
19.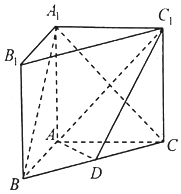 如图,在直三棱柱ABC-A1B1C1中,D为BC的中点,AB=3,AC=AA1=4,BC=5.
如图,在直三棱柱ABC-A1B1C1中,D为BC的中点,AB=3,AC=AA1=4,BC=5.(1)求证:AB⊥A1C;
(2)求证:A1B∥平面ADC1;
(3)求直三棱柱ABC-A1B1C1的体积.
分析 (1)在△ABC中,由已知结合勾股定理可得AB⊥AC.再由三棱柱ABC-A1B1C1为直三棱柱,可得AB⊥AA1,然后由线面垂直的判定可得AB⊥平面AA1C,进一步得到AB⊥A1C;
(2)设A1C与AC1交于E点,连接ED.由三角形中位线定理可得A1B∥ED,由线面平行的判定可得A1B∥平面ADC1;
(3)求出△ABC的面积$S=\frac{1}{2}×3×4=6$,直接由棱柱的体积公式求解.
解答 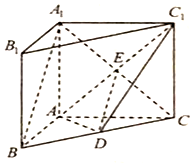 (1)证明:在△ABC中,AB=3,AC=4,BC=5,
(1)证明:在△ABC中,AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
∴AB⊥AC.
∵三棱柱ABC-A1B1C1为直三棱柱,
∴AA1⊥平面ABC,
∵AB?平面ABC,
∴AB⊥AA1,
∵AC∩AA1=A,
∴AB⊥平面AA1C,
∵A1C?平面AA1C,
∴AB⊥A1C;
(2)证明:设A1C与AC1交于E点,连接ED.
∵在△A1BC中,D为BC的中点,E为A1C的中点,
∴A1B∥ED,
∵ED?平面ADC1,A1B?平面ADC1,
∴A1B∥平面ADC1;
(3)解:∵△ABC的面积$S=\frac{1}{2}×3×4=6$,
直三棱柱ABC-A1B1C1的高h=4,
∴直三棱柱ABC-A1B1C1的体积V=Sh=6×4=24.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了柱、锥、台体体积的求法,是中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
9.已知复数z满足$\frac{z}{1+i}=1-i$(i为纯虚数),那么复数z=( )
| A. | 1 | B. | 2 | C. | i | D. | 2i |
10.已知函数$y=\frac{2}{x}$,当x由2变为1.5时,函数的增量为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{3}{2}$ |
4.在两坐标轴上截距均为m(m∈R)的直线l1与直线l2:2x+2y-3=0的距离为$\sqrt{2}$,则m=( )
| A. | $\frac{7}{2}$ | B. | 7 | C. | -$\frac{1}{2}$或$\frac{7}{2}$ | D. | -1或7 |
3.过点P(0,1),且与点A(3,3)和B(5,-1)的距离相等的直线方程是( )
| A. | y=1 | B. | 2x+y-1=0 | ||
| C. | y=1或2x+y-1=0 | D. | 2x+y-1=0或2x+y+1=0 |
20.在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的正弦值为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{{\sqrt{10}}}{4}$ | D. | $\frac{{\sqrt{6}}}{4}$ |