题目内容
1.函数f(x)=log4$\sqrt{x}$•log${\;}_{\sqrt{2}}$(2x)的值域用区间表示为[-$\frac{1}{8}$,+∞).分析 令t=log2x,则t∈R,y=f(x)=$\frac{1}{2}$(t2+t),结合二次函数的图象和性质,可得函数f(x)=log4$\sqrt{x}$•log${\;}_{\sqrt{2}}$(2x)的值域.
解答 解:函数f(x)=log4$\sqrt{x}$•log${\;}_{\sqrt{2}}$(2x)的定义域为(0,+∞),
由f(x)=log4$\sqrt{x}$•log${\;}_{\sqrt{2}}$(2x)=$\frac{1}{4}$log2x•2(log2x+1),
令t=log2x,则t∈R,
y=f(x)=$\frac{1}{2}$(t2+t),
当t=$-\frac{1}{2}$时,函数有最小值-$\frac{1}{8}$,无最大值,
故函数f(x)=log4$\sqrt{x}$•log${\;}_{\sqrt{2}}$(2x)的值域为[-$\frac{1}{8}$,+∞),
故答案为:[-$\frac{1}{8}$,+∞)
点评 本题考查的知识点是对数的运算性质,函数的最值,函数的值域,二次函数的图象和性质,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知一元二次不等式f(x)>0的解集为{x|x<-1或x>$\frac{1}{2}$},则f(10x)>0的解集为( )
| A. | {x|x<-1或x>lg2} | B. | {x|-1<x<lg2} | C. | {x|x>-lg2} | D. | {x|x<-lg2} |
11.若集合A={1,2,3,4},B={2,4,7,8},则集合A∪B等于.( )
| A. | {1,2,3,4} | B. | {1,3,4} | C. | {1,2,3,8,4,7} | D. | {0,1,2,3,4,7,8} |
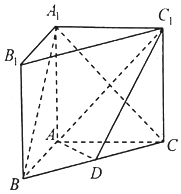 如图,在直三棱柱ABC-A1B1C1中,D为BC的中点,AB=3,AC=AA1=4,BC=5.
如图,在直三棱柱ABC-A1B1C1中,D为BC的中点,AB=3,AC=AA1=4,BC=5.