题目内容
3.过点P(0,1),且与点A(3,3)和B(5,-1)的距离相等的直线方程是( )| A. | y=1 | B. | 2x+y-1=0 | ||
| C. | y=1或2x+y-1=0 | D. | 2x+y-1=0或2x+y+1=0 |
分析 由题意可知当直线平行于直线AB时,或过AB的中点时满足题意,分别求其斜率可得方程.
解答 解:当直线平行于直线AB时,或过AB的中点时满足题意,
当直线平行于直线AB时,所求直线的斜率为k=$\frac{3+1}{3-5}$=-2,
故直线方程为y=-2x+1,即2x+y-1=0;
当直线过AB的中点(4,1)时,斜率为k=0,
故直线方程为y=1;
故所求直线方程是为:y=1或2x+y-1=0.
故选C.
点评 本题考查直线方程的求解,分类讨论是解决问题的关键,属基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1.若集合A={x∈Z|-2<x<2},B={x|y=log2x2},则A∩B=( )
| A. | {-1,1} | B. | {-1,0,1} | C. | {1} | D. | {0,1} |
6.在三棱锥P-ABC中,平面PAC⊥平面ABC,PA=PC=BA=BC,则直线PB与平面PAC所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
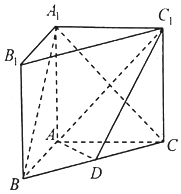 如图,在直三棱柱ABC-A1B1C1中,D为BC的中点,AB=3,AC=AA1=4,BC=5.
如图,在直三棱柱ABC-A1B1C1中,D为BC的中点,AB=3,AC=AA1=4,BC=5.