题目内容
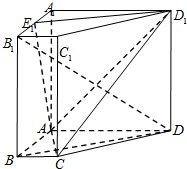 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.(Ⅰ)证明:B1D∥平面AD1E1;
(Ⅱ)若AC⊥BD,求平面ACD1和平面CDD1C1所成角(锐角)的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连结A1D交AD1于G,四边形ADD1A1为平行四边形,从而B1D∥E1G,由此能证明B1D∥平面AD1E1.
(Ⅱ)以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,求出平面ACD1的一个法向量和平面CDD1C1的一个法向量,由此利用向量法能求出平面ACD1和平面CDD1C1所成角(锐角)的余弦值.
(Ⅱ)以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,求出平面ACD1的一个法向量和平面CDD1C1的一个法向量,由此利用向量法能求出平面ACD1和平面CDD1C1所成角(锐角)的余弦值.
解答:
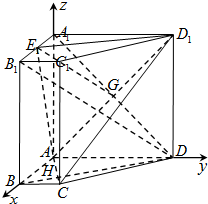 解:(Ⅰ)证明:连结A1D交AD1于G,
解:(Ⅰ)证明:连结A1D交AD1于G,
因为ABCD-A1B1C1D1为四棱柱,
所以四边形ADD1A1为平行四边形,
所以G为A1D的中点,
又E1为A1B1中点,所以E1G为△A1B1D的中位线,
从而B1D∥E1G…(4分)
又因为B1D?平面AD1E1,E1G?平面AD1E1,
所以B1D∥平面AD1E1. …(5分)
(Ⅱ)解:因为AA1⊥底面ABCD,AB?面ABCD,AD?面ABCD,
所以AA1⊥AB,AA1⊥AD,又∠BAD=90°,
所以AB,AD,AA1两两垂直.…(6分)
如图,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴,
建立空间直角坐标系.
设AB=t,则A(0,0,0),B(t,0,0),C(t,1,0),
D(0,3,0),C1(t,1,3),D1(0,3,3).
从而
=(t,1,0),
=(-t,3,0).
因为AC⊥BD,所以
•
=-t2+3+0=0,解得t=
.…(8分)
所以
=(0,3,3),
=(
,1,0).
设
=(x1,y1,z1)是平面ACD1的一个法向量,
则
即
令x1=1,则
=(1,-
,
).…(9分)
又
=(0,0,3),
=(-
,2,0).
设
=(x2,y2,z2)是平面CDD1C1的一个法向量,
则
即
令x2=1,则
=(1,
,0).…(10分)
∴cos<
,
>=
=
=
,
∴平面ACD1和平面CDD1C1所成角(锐角)的余弦值
.…(12分)
 解:(Ⅰ)证明:连结A1D交AD1于G,
解:(Ⅰ)证明:连结A1D交AD1于G,因为ABCD-A1B1C1D1为四棱柱,
所以四边形ADD1A1为平行四边形,
所以G为A1D的中点,
又E1为A1B1中点,所以E1G为△A1B1D的中位线,
从而B1D∥E1G…(4分)
又因为B1D?平面AD1E1,E1G?平面AD1E1,
所以B1D∥平面AD1E1. …(5分)
(Ⅱ)解:因为AA1⊥底面ABCD,AB?面ABCD,AD?面ABCD,
所以AA1⊥AB,AA1⊥AD,又∠BAD=90°,
所以AB,AD,AA1两两垂直.…(6分)
如图,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴,
建立空间直角坐标系.
设AB=t,则A(0,0,0),B(t,0,0),C(t,1,0),
D(0,3,0),C1(t,1,3),D1(0,3,3).
从而
| AC |
| BD |
因为AC⊥BD,所以
| AC |
| BD |
| 3 |
所以
| AD1 |
| AC |
| 3 |
设
| n1 |
则
|
|
令x1=1,则
| n1 |
| 3 |
| 3 |
又
| CC1 |
| CD |
| 3 |
设
| n2 |
则
|
|
令x2=1,则
| n2 |
| ||
| 2 |
∴cos<
| n1 |
| n2 |
|
| ||||
|
|
|1×1+
| ||||||||
|
| 1 |
| 7 |
∴平面ACD1和平面CDD1C1所成角(锐角)的余弦值
| 1 |
| 7 |
点评:本小题考查空间中直线与平面的位置关系、空间向量的应用等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想、函数与方程思想.

练习册系列答案
相关题目
已知全集U=R,集合A={x||x-1|≤2},CUB=(-∞,1)∪[4,+∞),则A∪B=( )
| A、[1,3] |
| B、(1,3] |
| C、[-1,4] |
| D、[-1,4) |
若函数y=x2-4x-4的定义域为[0,m],值域为[-8,-4],则m的取值范围是( )
| A、(2,4) |
| B、[2,4) |
| C、(2,4] |
| D、[2,4] |
某班组织文艺晚会,准备从A,B等8个节目中选出4个节目演出,要求:A,B两个节目至少有一个选中,且A,B同时选中时,它们的演出顺序不能相邻,那么不同演出顺序的和数为( )
| A、1860 | B、1320 |
| C、1140 | D、1020 |
在等比数例{an}中,2a4,a6,48成等差数列,且a3•a5=64,则{an}的前8项和为( )
| A、255 | B、85 |
| C、255或-85 | D、255或85 |
在△ABC中,AB=4,∠ABC=30°,D是边BC上的一点,且
•
=
•
,则
•
的值为( )
| AD |
| AB |
| AD |
| AC |
| AD |
| AB |
| A、0 | B、4 | C、8 | D、-4 |
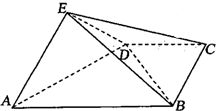 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
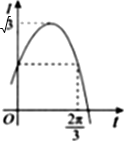
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点. 已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<
已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<