题目内容
已知函数f(x)=
cos(x+
),x∈R.
(1)求函数f(x)的最小正周期和值域;
(2)若θ∈(0,
),且f(θ)=
,求sin2θ的值.
| 2 |
| π |
| 4 |
(1)求函数f(x)的最小正周期和值域;
(2)若θ∈(0,
| π |
| 2 |
| 1 |
| 2 |
考点:三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)根据f(x)=
cos(x+
),可得函数f(x)的最小正周期以及值域.
(2)根据f(θ)=
,求得cos(θ+
)=
,再根据sin2θ=-cos(
+2θ)=1-2cos2(θ+
),计算求得结果.
| 2 |
| π |
| 4 |
(2)根据f(θ)=
| 1 |
| 2 |
| π |
| 4 |
| ||
| 4 |
| π |
| 2 |
| π |
| 4 |
解答:
解:(1)∵f(x)=
cos(x+
),∴函数f(x)的最小正周期为2π.
∵x∈R,cos(x+
)∈[-1,1],∴
cos(x+
)∈[-
,
],
即函数f(x)的值域为[-
,
].
(2)∵f(θ)=
,∴
cos(θ+
)=
,∴cos(θ+
)=
,
∴sin2θ=-cos(
+2θ)=1-2cos2(θ+
)=1-2×(
)2=
.
| 2 |
| π |
| 4 |
∵x∈R,cos(x+
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
| 2 |
即函数f(x)的值域为[-
| 2 |
| 2 |
(2)∵f(θ)=
| 1 |
| 2 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| ||
| 4 |
∴sin2θ=-cos(
| π |
| 2 |
| π |
| 4 |
| ||
| 4 |
| 3 |
| 4 |
点评:本题主要考查正弦函数的周期性、值域以及二倍角公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知四棱锥P-ABCD中,侧面PAD为等边三角形,底面平行四边形ABCD⊥平面PAD,且PA=2
如图,已知四棱锥P-ABCD中,侧面PAD为等边三角形,底面平行四边形ABCD⊥平面PAD,且PA=2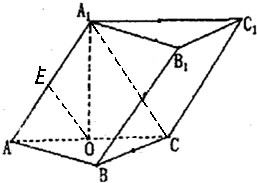 如图,三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,△A1AC,△ABC均为正三角形,点O,E分别为AC,AA1中点.求二面角C1-AB-C的余弦值.
如图,三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,△A1AC,△ABC均为正三角形,点O,E分别为AC,AA1中点.求二面角C1-AB-C的余弦值.