题目内容
已知函数f（x）=x3+ax2+bx+c，0＜f（-1）=f（-2）=f（-3）≤3，求c的取值范围．
考点：利用导数研究函数的单调性
专题：函数的性质及应用
分析：由f（-1）=f（-2）=f（-3）列出方程组求出a，b代入0＜f（-1）≤3求出c的范围
解答：
解：由f（-1）=f（-2）=f（-3）得
，
解得
，则f（x）=x3+6x2+11x+c，
由0＜f（-1）≤3，得0＜-1+6-11+c≤3，
即6＜c≤9．
|
解得
|
由0＜f（-1）≤3，得0＜-1+6-11+c≤3，
即6＜c≤9．
点评：本题主要考查函数解析式的求解，以及不等式的应用，求出a，b的值是解决本题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
如图，E，F分别在矩形ABCD的边AD，BC上，AB=2，AD=5，AE=1，BF=3，现将四边形AEFB沿EF折起到A′EFB′，使DF⊥B′F．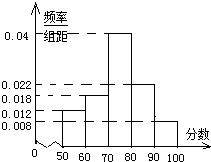
某次素质测试，随机抽取了部分学生的成绩，得到如图所示的频率分布直方图．