题目内容
如图，E，F分别在矩形ABCD的边AD，BC上，AB=2，AD=5，AE=1，BF=3，现将四边形AEFB沿EF折起到A′EFB′，使DF⊥B′F．（Ⅰ）求证：A′E∥平面B′DF
（Ⅱ）求证：平面A′EFB′⊥平面CDEF；
（Ⅲ）求直线B′D与平面A′EFB′所成角的余弦值．
考点：直线与平面所成的角,直线与平面平行的判定,平面与平面垂直的判定
专题：综合题,空间位置关系与距离,空间角
分析：（I）折叠前AE∥BF，折叠后A′E∥B′F，利用线面平行的判定定理，可得A′E∥平面B′DF；
（Ⅱ）根据折叠前线段的长度，判定EF与DF的垂直关系，再利用线线垂直⇒线面垂直，然后由线面垂直⇒面面垂直．
（Ⅲ）由DF⊥平面A′EFB′，可得∠DB′F为直线B′D与平面A′EFB′所成角，从而可求直线B′D与平面A′EFB′所成角的余弦值．
（Ⅱ）根据折叠前线段的长度，判定EF与DF的垂直关系，再利用线线垂直⇒线面垂直，然后由线面垂直⇒面面垂直．
（Ⅲ）由DF⊥平面A′EFB′，可得∠DB′F为直线B′D与平面A′EFB′所成角，从而可求直线B′D与平面A′EFB′所成角的余弦值．
解答：
（I）证明：折叠前AE∥BF，折叠后A′E∥B′F，
∵A′E?平面B′DF，B′F?平面B′DF
∴A′E∥平面B′DF；
（Ⅱ）证明：∵DF=EF=2
，ED=4，
∴EF⊥DF，又∵DF⊥B′F，EF∩B′F=F，
∴DF⊥平面A′EFB′，又DF?平面CDEF，
∴平面A′EFB′⊥平面CDEF；
（Ⅲ）解：∵DF⊥平面A′EFB′，
∴∠DB′F为直线B′D与平面A′EFB′所成角，
由B′F=BF=3，DF=2
，∴B′D=
，
∴cos∠DB′F=
=
，
即直线B′D与平面A′EFB′所成角的余弦值为
．
∵A′E?平面B′DF，B′F?平面B′DF
∴A′E∥平面B′DF；
（Ⅱ）证明：∵DF=EF=2
| 2 |
∴EF⊥DF，又∵DF⊥B′F，EF∩B′F=F，
∴DF⊥平面A′EFB′，又DF?平面CDEF，
∴平面A′EFB′⊥平面CDEF；
（Ⅲ）解：∵DF⊥平面A′EFB′，
∴∠DB′F为直线B′D与平面A′EFB′所成角，
由B′F=BF=3，DF=2
| 2 |
| 17 |
∴cos∠DB′F=
| B′F |
| B′D |
3
| ||
| 17 |
即直线B′D与平面A′EFB′所成角的余弦值为
3
| ||
| 17 |
点评：本题考查直线与平面平行、平面与平面垂直的证明，考查线面角的大小的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
一本好题口算题卡系列答案
相关题目
已知数列{2n-11}，则Sn的最小值为（ ）
| A、S1 |
| B、S5 |
| C、S6 |
| D、S11 |
对于R上可导的任意函数f（x），若满足（x-3）f′（x）≥0，则必有（ ）
| A、f（0）+f（5）＜2f（3） |
| B、f（0）+f（5）≤2f（3） |
| C、f（0）+f（5）≥2f（3） |
| D、f（0）+f（5）＞2f（3） |
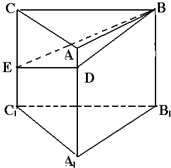如图，已知体积为8，高为4的三棱柱ABC-A1B1C1，CC1⊥平面A1B1C1，点D、E分别在棱AA1和CC1上，且DE⊥B1C1，DA1=3，EC1=2．