题目内容
在数列{an}中,an=(2n-3)×(
)n,求数列的前n项和Sn.
| 1 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:利用错位相减求和法求解.
解答:
解:∵an=(2n-3)×(
)n,
∴Sn=(-1)×
+1×(
)2+3×(
)3+…+(2n-3)×(
)n,①
Sn=(-1)×(
)2+1×(
)3+3×(
)4+…+(2n-3)×(
)n+1,②
①-②,得-
Sn=-
+
+
+
+…+
-(2n-3)×(
)n+1
=-
+
-(2n-3)×(
)n+1
=
-
-(2n-3)×(
)n+1,
∴Sn=(2n+1)×(
)n-1.
| 1 |
| 2 |
∴Sn=(-1)×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②,得-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2 |
∴Sn=(2n+1)×(
| 1 |
| 2 |
点评:本题考查数列的前n项和的求法,是中档题,解题时要注意错位相减法的合理运用.

练习册系列答案
相关题目
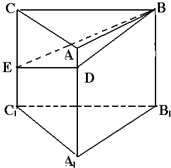 如图,已知体积为8,高为4的三棱柱ABC-A1B1C1,CC1⊥平面A1B1C1,点D、E分别在棱AA1和CC1上,且DE⊥B1C1,DA1=3,EC1=2.
如图,已知体积为8,高为4的三棱柱ABC-A1B1C1,CC1⊥平面A1B1C1,点D、E分别在棱AA1和CC1上,且DE⊥B1C1,DA1=3,EC1=2. 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,侧面B1C1CB⊥底面ABC,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,侧面B1C1CB⊥底面ABC,且AC1⊥BC.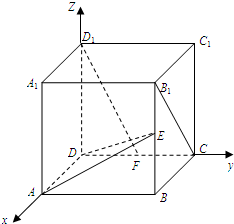 如图,在正方体ABCD-A1B1C1D1中,AB=2,E,F分别是BB1,CD的中点,(如图建立空间直角坐标系)
如图,在正方体ABCD-A1B1C1D1中,AB=2,E,F分别是BB1,CD的中点,(如图建立空间直角坐标系)