题目内容
已知函数f(x)=ax2-4lnx,a∈R.
(1)当a=
时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)论f(x)的单调性.
(1)当a=
| 1 |
| 2 |
(2)论f(x)的单调性.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,导数的综合应用
分析:(1)当a=
时,f(x)=
x2-4lnx的定义域为(0,+∞);求导f′(x)=x-
;从而求切线方程;
(2)求导f′(x)=ax-
=
;讨论a以确定函数的单调性的判断.
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| x |
(2)求导f′(x)=ax-
| 4 |
| x |
| ax2-4 |
| x |
解答:
解:(1)当a=
时,f(x)=
x2-4lnx的定义域为(0,+∞);
f′(x)=x-
;
则f′(1)=1-4=-3,f(1)=
;
故曲线y=f(x)在点(1,f(1))处的切线方程为
y=-3(x-1)+
;
故6x+2y-7=0;
(2)f′(x)=ax-
=
;
当a≤0时,f′(x)<0;
故函数f(x)=ax2-4lnx在(0,+∞)上是减函数,
当a>0时,x∈(0,
)时,f′(x)<0;
x∈(
,+∞)时,f′(x)>0;
故f(x)在(0,
)上是减函数,在(
,+∞)上是增函数.
| 1 |
| 2 |
| 1 |
| 2 |
f′(x)=x-
| 4 |
| x |
则f′(1)=1-4=-3,f(1)=
| 1 |
| 2 |
故曲线y=f(x)在点(1,f(1))处的切线方程为
y=-3(x-1)+
| 1 |
| 2 |
故6x+2y-7=0;
(2)f′(x)=ax-
| 4 |
| x |
| ax2-4 |
| x |
当a≤0时,f′(x)<0;
故函数f(x)=ax2-4lnx在(0,+∞)上是减函数,
当a>0时,x∈(0,
2
| ||
| a |
x∈(
2
| ||
| a |
故f(x)在(0,
2
| ||
| a |
2
| ||
| a |
点评:本题考查了导数的综合应用及导数的几何意义的应用,属于中档题.

练习册系列答案
相关题目
函数y=
的定义域为( )
| 4x |
| A、[0,+∞) |
| B、(0,+∞) |
| C、{0} |
| D、以上答案都不对 |
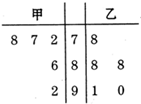 甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是
甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从2014年到2017年期间,甲计划每年6月6日都到银行存入a元的一个定期储蓄,若年利率q保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,若到2017年6月6日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
| A、a(1+q)3 | ||
| B、a(1+q)5 | ||
C、
| ||
D、
|