Question

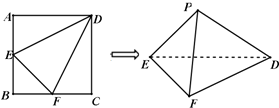如图，在边长为2的正方形ABCD中，E，F分别是AB，BC的中点，将△AED，△BEF，△CFD分别沿DE，EF，DF折起，使A，B，C三点重合于点P．
（Ⅰ）求证：平面PDE⊥平面PEF；
（Ⅱ）求P到平面DEF的距离．

Answer 1

考点：直线与平面所成的角,平面与平面垂直的判定

专题：空间位置关系与距离

分析：（Ⅰ）由已知∠A=∠B=∠C=90°，PD⊥PE，PD⊥PF，PE⊥PF，由此能证明PD⊥平面PEF，平面PDE⊥平面PEF．
（Ⅱ）设P到平面DEF的距离为d，由V_P-DEF=V_D-PEF，能求出P到平面DEF的距离．

解答： （Ⅰ）证明：由已知四边形ABCD是正方形，
∴∠A=∠B=∠C=90°，
又折叠后A，B，C三点重合于点P，
∴PD⊥PE，PD⊥PF，PE⊥PF，
又PE∩PF=P，∴PD⊥平面PEF，…（4分）
又PD?平面PDE，
∴平面PDE⊥平面PEF．…（6分）
（Ⅱ）解：PD=2，PE=PF=1，EF=

2

，DE=DF=

5

，
S_△DEF=

1

2

×

2

×

5- 1 2

=

3

2

，设P到平面DEF的距离为d，
由V_P-DEF=V_D-PEF，得

1

3

×S_△DEF×d=

1

3

×S_△PEF×PD，…（9分）
∴

1

3

×

3

2

×d=

1

3

×

1

2

×1×1×2，∴d=

2

3

，
∴P到平面DEF的距离为

2

3

．…（12分）

点评：本题考查平面与平面垂直的证明，考查点到平面的距离的求法，解题时要认真审题，注意空间思维能力的培养．