题目内容
3.要得到函数$y=sin({\frac{x}{2}-\frac{π}{4}})$的图象,只需将y=sin$\frac{x}{2}$的图象( )| A. | 向左平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
分析 利用平移原则求解即可得解.
解答 解:函数y=sin($\frac{x}{2}$-$\frac{π}{4}$)=sin$\frac{1}{2}$(x-$\frac{π}{2}$),
只需将y=sin$\frac{1}{2}$x的图象向右平移$\frac{π}{2}$个单位,即可得到函数y=sin($\frac{x}{2}$-$\frac{π}{4}$)的图象,
故选:B.
点评 本题考查三角函数的图象的平移,注意自变量x的系数,属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
15.若θ∈(0,π),且sinθ+cosθ=$\frac{1}{5}$,则曲线$\frac{{x}^{2}}{sinθ}$+$\frac{{y}^{2}}{cosθ}$=1是( )
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
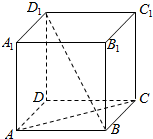 如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.