题目内容
11.设θ是第三象限角,且|sin$\frac{θ}{2}$|=-sin$\frac{θ}{2}$,则$\frac{θ}{2}$是第四象限角.分析 θ是第三象限角,可得$2kπ+π<θ<2kπ+\frac{3π}{2}$,解得$kπ+\frac{π}{2}$<$\frac{θ}{2}$<kπ$+\frac{3π}{4}$,k∈Z.对k分类讨论即可得出.
解答 解:∵θ是第三象限角,
∴$2kπ+π<θ<2kπ+\frac{3π}{2}$,
解得$kπ+\frac{π}{2}$<$\frac{θ}{2}$<kπ$+\frac{3π}{4}$,k∈Z.
当k为偶数时,$\frac{θ}{2}$位于第二象限;
当k为奇数时,$\frac{θ}{2}$位于第四象限,且满足|sin$\frac{θ}{2}$|=-sin$\frac{θ}{2}$,
因此$\frac{θ}{2}$是第四象限角.
故答案为:四.
点评 本题考查了象限角、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.在△ABC中,已知a=2,A=45°,B=120°,则b=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
2.方程y=k(x-1)表示( )
| A. | 过点(-1,0)的所有直线 | B. | 过点(1,0)的所有直线 | ||
| C. | 过点(1,0)且不垂直于x轴的所有直线 | D. | 过点(1,0)且除去x轴的所有直线 |
19.已知集合A={1,4,x},B={1,x2},且B⊆A,则满足条件的实数x有( )
| A. | 1 个 | B. | 2 个 | C. | 3个 | D. | 4个 |
16.运行如图所示的程序框图,若输出结果为$\frac{15}{8}$,则判断框中应该填的条件是( )
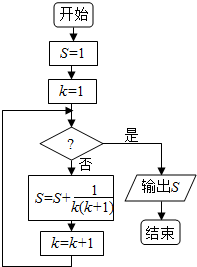

| A. | k>5 | B. | k>6 | C. | k>7 | D. | k>8 |
3.要得到函数$y=sin({\frac{x}{2}-\frac{π}{4}})$的图象,只需将y=sin$\frac{x}{2}$的图象( )
| A. | 向左平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
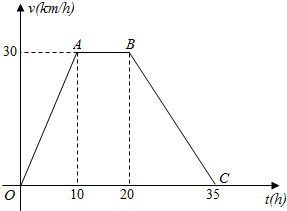 据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).