题目内容
12.已知点P是圆x2+y2=1上动点,定点Q(6,0),点M是线段PQ靠近Q点的三等分点,则点M的轨迹方程是( )| A. | (x+3)2+y2=4 | B. | (x-4)2+y2=$\frac{1}{9}$ | C. | (2x-3)2+4y2=1 | D. | (2x+3)2+4y2=1 |
分析 点M是靠近点Q的三等分点,设M(x,y),则P(3x,3y-8),代入圆的方程即得M的轨迹方程.
解答 解:点M是靠近点Q的三等分点,设M(x,y),P(x′,y′),
$\overrightarrow{QP}$=3$\overrightarrow{QM}$,则P(3x-12,3y),代入圆的方程得(3x-12)2+(3y)2=1.
M的轨迹方程是:(x-4)2+y2=$\frac{1}{9}$.
故选:B.
点评 求曲线的轨迹方程常采用的方法有直接法、定义法、相关点代入法、参数法,本题主要是利用相关点代入法,根据相关点所满足的方程,通过转换而求动点的轨迹方程.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
2.6人排成一排,其中甲乙必须排在一起,丙丁不能排在一起,则不同的排法有( )种.
| A. | 72 | B. | 144 | C. | 240 | D. | 480 |
3.△A BC是边长为2的等边三角形,已知向量$\vec a$,$\vec b$满足$\overrightarrow{{A}{B}}=2\vec a$,$\overrightarrow{{A}C}=2\vec a+\vec b$,则下列结论不正确的是( )
| A. | $|{\overrightarrow b}|=2$ | B. | $\overrightarrow a•\overrightarrow b=-1$ | C. | $|{\overrightarrow a+\overrightarrow b}|=\sqrt{7}$ | D. | $({4\overrightarrow a+\overrightarrow b})⊥\overrightarrow b$ |
17.1340°角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
2.为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):
(1)求a,b,c的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
| 社团名称 | 成员人数 | 抽取人数 |
| 话剧社 | 50 | a |
| 创客社 | 150 | b |
| 演讲社 | 100 | c |
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
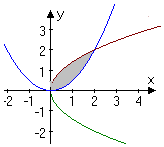 已知曲线C1:y2=2x与C2:y=$\frac{1}{2}{x^2}$.求两条曲线所围图形(如图所示阴影部分)的面积S.
已知曲线C1:y2=2x与C2:y=$\frac{1}{2}{x^2}$.求两条曲线所围图形(如图所示阴影部分)的面积S.