题目内容
9.已知两点A(2,2),B(2,1),O为坐标原点,若|$\overrightarrow{OA}$-t$\overrightarrow{OB}$|≤$\frac{2\sqrt{5}}{5}$,则实数t的值为( )| A. | $\frac{6}{5}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{4}{3}$ |
分析 求出$\overrightarrow{OA}-t\overrightarrow{OB}$的坐标,代入向量的模长公式,列不等式解出t.
解答 解:$\overrightarrow{OA}-t\overrightarrow{OB}$=(2-2t,2-t),
∴|$\overrightarrow{OA}-t\overrightarrow{OB}$|=$\sqrt{(2-2t)^{2}+(2-t)^{2}}$≤$\frac{2\sqrt{5}}{5}$,
化简得:5t2-12t+$\frac{36}{5}$≤0,
解得t=$\frac{6}{5}$.
故选A.
点评 本题考查了平面向量的坐标运算,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
17.1340°角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
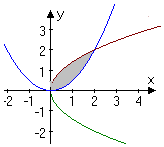 已知曲线C1:y2=2x与C2:y=$\frac{1}{2}{x^2}$.求两条曲线所围图形(如图所示阴影部分)的面积S.
已知曲线C1:y2=2x与C2:y=$\frac{1}{2}{x^2}$.求两条曲线所围图形(如图所示阴影部分)的面积S.