题目内容
15．用一个平面去截一个几何体，得到的截面是平面四边形，这个几何体不可能是（ ）| A． | 三棱锥 | B． | 棱柱 | C． | 四棱台 | D． | 球 |
分析 用一个平面去截一个球，得到的截面圆．
解答 解：用一个平面去截一个几何体，得到的截面是平面四边形，
在三棱锥、棱柱、四棱台、球四个选中，知：
这个几何体不可能是球．
故选：D．
点评 本题考是截面图形的判断，是基础题，解题时要认真审题，注意球的结构特征的合理运用．
练习册系列答案
相关题目
5．已知函数f（x）=$\left\{\begin{array}{l}{x+1，x≥0}\\{{x}^{2}，x＜0}\end{array}\right.$，则f[f（2）]的值为（ ）
| A． | -1 | B． | 1 | C． | 4 | D． | 5 |
6．函数f（x）=2x3在点（-1，f（-1））处的切线方程为（ ）
| A． | y=6x+4 | B． | y=6x-4 | C． | y=-6x+4 | D． | y=-6x-4 |
3．△A BC是边长为2的等边三角形，已知向量$\vec a$，$\vec b$满足$\overrightarrow{{A}{B}}=2\vec a$，$\overrightarrow{{A}C}=2\vec a+\vec b$，则下列结论不正确的是（ ）
| A． | $|{\overrightarrow b}|=2$ | B． | $\overrightarrow a•\overrightarrow b=-1$ | C． | $|{\overrightarrow a+\overrightarrow b}|=\sqrt{7}$ | D． | $（{4\overrightarrow a+\overrightarrow b}）⊥\overrightarrow b$ |
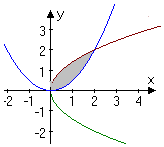已知曲线C1：y2=2x与C2：y=$\frac{1}{2}{x^2}$．求两条曲线所围图形（如图所示阴影部分）的面积S．