题目内容
椭圆C1:
+
=1(a>b>0)的左、右焦点分别为F1、F2,右顶点为A,P为椭圆C1上任意一点.
(1)求
•
的最大值;
(2)设双曲线C2以椭圆C1的焦点为顶点,顶点为焦点,B是双曲线C2在第一象限上任意一点,当
•
的最大值为3c2时,是否存在常数λ(λ>0),使得∠BAF1=λ∠BF1A恒成立?若存在,求出λ的值;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求
| PF1 |
| PF2 |
(2)设双曲线C2以椭圆C1的焦点为顶点,顶点为焦点,B是双曲线C2在第一象限上任意一点,当
| PF1 |
| PF2 |
考点:椭圆的简单性质
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:(1)由题意,F1(-c,0),F2(c,0),P(x,y),从而表示出向量
,
;进而求
•
的最大值;
(2)双曲线方程为3x2-y2=3c2,设动点B(m,n)(m>c),表示出向量
=(m+c,n),
=(3c,0),
=(m-2c,n),
=(-3c,0),从而求出cos∠BAF1,cos∠BF1A;从而求出λ的值.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
(2)双曲线方程为3x2-y2=3c2,设动点B(m,n)(m>c),表示出向量
| F1B |
| F1A |
| AB |
| AF1 |
解答:
解:(1)由题意,F1(-c,0),F2(c,0),P(x,y);
则
=(-c-x,-y),
=(c-x,-y),
则
•
=x2+y2-c2=x2+b2-
x2-c2
=(1-
)x2+b2-c2,
则当x=a或x=-a时,
•
有最大值,
•
=a2-c2=b2.
(2)当b2=3c2时,
可得双曲线方程为3x2-y2=3c2,
设动点B(m,n)(m>c),
则有n2=3(m2-c2),
=(m+c,n),
=(3c,0),
=(m-2c,n),
=(-3c,0),
于是:cos∠BAF1=
=
=
,
cos∠BF1A=
=
,
∵2cos2∠BF1A-1=
-1=
=cos∠BAF1,
∴∠BAF1=2∠BF1A,
即λ=2.
则
| PF1 |
| PF2 |
则
| PF1 |
| PF2 |
| b2 |
| a2 |
=(1-
| b2 |
| a2 |
则当x=a或x=-a时,
| PF1 |
| PF2 |
| PF1 |
| PF2 |
(2)当b2=3c2时,
可得双曲线方程为3x2-y2=3c2,
设动点B(m,n)(m>c),
则有n2=3(m2-c2),
| F1B |
| F1A |
| AB |
| AF1 |
于是:cos∠BAF1=
| -(m-2c) | ||
|
| 2c-m | ||
|
| 2c-m |
| 2m-c |
cos∠BF1A=
| m+c | ||
|
| m+c | ||
|
∵2cos2∠BF1A-1=
| 2m2+4mc+2c2 |
| 4m2+2cm-2c2 |
| 2c-m |
| 2m-c |
∴∠BAF1=2∠BF1A,
即λ=2.
点评:本题考查了平面向量的应用,同时考查了椭圆的性质,属于中档题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
下列命题中的假命题是( )
A、?x∈R,sinx=
| ||||
| B、?x∈R,log2x=1 | ||||
C、?x∈R,(
| ||||
| D、?x∈R,x2≥0 |
已知x,y之间的几组数据如下表:
假设根据上表数据所得线性回归方程为y=b1x+a1,某同学根据上表中前两组数据求得的直线方程为y=b2x+a2,则以下结论正确的是( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
| A、b1>b2,a1>a2 |
| B、b1>b2,a1<a2 |
| C、b1<b2,a1>a2 |
| D、b1<b2,a1<a2 |
函数f(x)=-x2+2ax+3在区间(-∞,4)上单调递增,则a的取值范围是( )
| A、a<4 | B、a≤4 |
| C、a>4 | D、a≥4 |
若菱形ABCD的边长为2,则|
-
+
|等于( )
| AB |
| CB |
| CD |
| A、2 | ||
| B、1 | ||
C、2
| ||
D、
|
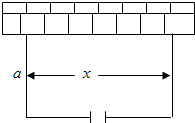 某动物园要围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).
某动物园要围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).