题目内容

A、B、C、D、E五人并排站成一排，若A，B必须相邻，那么不同的排法共有
 
种．
考点：计数原理的应用
专题：应用题,排列组合
分析：A，B两人必须相邻，利用捆绑法与其余3人全排即可．
解答： 解：由题意，利用捆绑法，A，B必须相邻的方法数为A22•A44=48种．
故答案为：48
点评：本题主要考查排列与组合及两个基本原理，正确运用捆绑法是关键．
练习册系列答案
相关题目
已知向量|
a
|=|
b
|=2，且
a
•
b
=2，则|
a
+
b
|=
 
．
若函数f（x）=
k-2x
1+k•2x
（k为常数）在定义域上为奇函数．
（1）求k的值；
（2）若k＞0，且对任意的实数t∈[-3，-2]，不等式f（2t-t2）+f（2t2-m）＜0恒成立，求实数m的取值范围．
已知f（x）是奇函数，g（x）是偶函数，且f（x）+g（x）=ex-kx，k为常数．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若k≤1，证明：f（x）在R上为增函数．
（
4
5
）0-（1-0.5-2）÷(3
3
8
)
1
3
=
 
．
已知函数f（x）是定义在（-6，6）上的偶函数，f（x）在[0，6）上是单调函数，且f（-2）＜f（1）则下列不等式成立的是（　　）
A、f（-1）＜f（1）＜f（3）
B、f（2）＜f（3）＜f（-4）
C、f（-2）＜f（0）＜f（1）
D、f（5）＜f（-3）＜f（-1）
已知等边△ABC的边长为1，且满足
CP
-2
CB
-3
CA
=
0
，则
PA
•
PB
=（　　）
A、3B、12C、-3D、-12
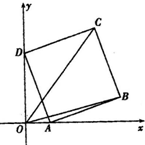把边长为1的正方形ABCD如图放置，A、D别在x轴、y轴的非负半轴上滑动．
（1）当A点与原点重合时，
OB
•
OC
=
 
；
（2）
OB
•
OC
的最大值是
 
．
已知O为坐标原点，对于函数f（x）=asinx+bcosx，称向量
OM
=（a，b）为函数f（x）的伴随向量，设函数g（x）=
3
sin(
π
2
+x)+cos(
π
2
-x)，
（Ⅰ）求g（x）的伴随向量
OM
的模；
（Ⅱ）若h（x）=g2（x），求h（x）在[0，
π
2
]内的最值及对应x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网