Question

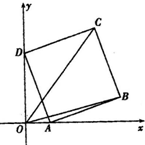把边长为1的正方形ABCD如图放置，A、D别在x轴、y轴的非负半轴上滑动．
（1）当A点与原点重合时，

OB

•

OC

=

 

；
（2）

OB

•

OC

的最大值是

 

．

Answer 1

考点：平面向量数量积的运算

专题：计算题,平面向量及应用

分析：（1）求出B，C的坐标，以及向量OB，OC的坐标，再由数量积的坐标公式即可得到；
（2）令∠OAD=θ，由边长为1的正方形ABCD的顶点A、D分别在x轴、y轴正半轴上，可得出B，C的坐标，由此可以表示出两个向量，算出它们的内积．

解答： 解：（1）当A点与原点重合时，B在x轴上，B（1，0），C（1，1），
则

OB

•

OC

=（1，0）•（1，1）=1；
（2）如图令∠OAD=θ，由于AD=1故0A=cosθ，OD=sinθ，
如图∠BAX=

π

2

-θ，AB=1，
故x_B=cosθ+cos（

π

2

-θ）=cosθ+sinθ，y_B=sin（

π

2

-θ）=cosθ，
故

OB

=（cosθ+sinθ，cosθ）
同理可求得C（sinθ，cosθ+sinθ），即

OC

=（sinθ，cosθ+sinθ），
∴

OB

•

OC

=（cosθ+sinθ，cosθ）•（sinθ，cosθ+sinθ）=1+sin2θ，
当θ=45°时，sin2θ取最大1，则

OB

•

OC

的最大值是2．
故答案为：1，2

点评：本题考查平面向量及运用，考查向量的数量积的坐标运算，同时考查三角函数的最值，属于中档题．