题目内容
已知f(x)是奇函数,g(x)是偶函数,且f(x)+g(x)=ex-kx,k为常数.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若k≤1,证明:f(x)在R上为增函数.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若k≤1,证明:f(x)在R上为增函数.
考点:函数单调性的判断与证明,函数解析式的求解及常用方法
专题:函数的性质及应用,导数的综合应用
分析:(Ⅰ)根据奇函数、偶函数的定义,对于f(x)+g(x)=ex-kx,把x换上-x,便可得到:-f(x)+g(x)=
+kx,两式联立即可解出f(x)=
-
-kx;
(Ⅱ)求f′(x)=
,对于(ex)2-2kx+1,令ex=t(t>0),便得到函数y=t2-2kt+1.若求该函数的判别式,容易发现需对k分成-1≤k≤1,和k<-1两种情况判断y的符号,并需证明在这两种情况下的y都大于等于0,从而便证出k≤1时,f(x)在R上为增函数.
| 1 |
| ex |
| ex |
| 2 |
| 1 |
| 2ex |
(Ⅱ)求f′(x)=
| (ex)2-2kex+1 |
| 2ex |
解答:
解:(Ⅰ)由已知条件得:f(-x)=-f(x),g(-x)=g(x),-f(x)+g(x)=
+kx;
∴由
得,f(x)=
-
-kx;
(Ⅱ)证明:f′(x)=
;
对于(ex)2-2kex+1,设ex=t(t>0),y=t2-2kt+1;
①当-1≤k≤1时,△=4(k2-1)≤0;
∴y≥0,即f′(x)≥0;
∴f(x)在R上为增函数;
②当k<-1时,函数y=t2-2kt+1,t>0,的对称轴为x=k,则:
该函数在[0,+∞)为增函数,且t=0时,y=1>0;
∴对于任意的t>0,y>0;
即对于任意的x∈R,f′(x)>0;
∴f(x)在R上为增函数;
综合①②得若k≤1,f(x)在R上为增函数.
| 1 |
| ex |
∴由
|
| ex |
| 2 |
| 1 |
| 2ex |
(Ⅱ)证明:f′(x)=
| (ex)2-2kex+1 |
| 2ex |
对于(ex)2-2kex+1,设ex=t(t>0),y=t2-2kt+1;
①当-1≤k≤1时,△=4(k2-1)≤0;
∴y≥0,即f′(x)≥0;
∴f(x)在R上为增函数;
②当k<-1时,函数y=t2-2kt+1,t>0,的对称轴为x=k,则:
该函数在[0,+∞)为增函数,且t=0时,y=1>0;
∴对于任意的t>0,y>0;
即对于任意的x∈R,f′(x)>0;
∴f(x)在R上为增函数;
综合①②得若k≤1,f(x)在R上为增函数.
点评:考查奇函数、偶函数的定义,以及函数导数符号和函数单调性的关系,二次函数取值情况和判别式△的关系,二次函数的单调性.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
函数f(x)=2x+x2-2在区间(0,1)内的零点个数是( )
| A、0 | B、1 | C、2 | D、3 |
对于函数f(x)=2x,总有( )
A、f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
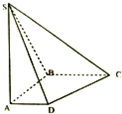 在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD= 一次学科测试成绩的频率分布直方图都受到不同程度的污损,可见部分如图.已知50~60分的有两个数,60~70分的有7个数,70~80分的有10个数,
一次学科测试成绩的频率分布直方图都受到不同程度的污损,可见部分如图.已知50~60分的有两个数,60~70分的有7个数,70~80分的有10个数,