题目内容
已知A,B,C是△ABC的三个内角,且满足sin2A-sin2B+sin2C=
sinAsinC
(Ⅰ)求角B;
(Ⅱ)若sinA=
,求cosC的值.
| 2 |
(Ⅰ)求角B;
(Ⅱ)若sinA=
| 3 |
| 5 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(Ⅰ)已知等式利用正弦定理化简,得到关系式,再利用余弦定理表示出cosB,将得出的关系式代入求出cosB的值,即可确定出角B的度数;
(Ⅱ)由sinA的值求出cosA的值,根据B的度数得到A+C的度数,表示出C,代入cosC中,利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
(Ⅱ)由sinA的值求出cosA的值,根据B的度数得到A+C的度数,表示出C,代入cosC中,利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
解答:
解:(Ⅰ)∵△ABC中,sin2A-sin2B+sin2C=
sinAsinC,
∴由正弦定理化简得:a2+c2-b2=
ac,
∴cosB=
=
,
∴B=
;
(Ⅱ)∵B=
,sinA=
<
,
∴A<B,A+C=
,
∴cosA=
=
,
则cosC=cos(
-A)=cos
cosA+sin
sinA=-
×
+
×
=-
.
| 2 |
∴由正弦定理化简得:a2+c2-b2=
| 2 |
∴cosB=
| a2+c2-b2 |
| 2ac |
| ||
| 2 |
∴B=
| π |
| 4 |
(Ⅱ)∵B=
| π |
| 4 |
| 3 |
| 5 |
| ||
| 2 |
∴A<B,A+C=
| 3π |
| 4 |
∴cosA=
| 1-sin2A |
| 4 |
| 5 |
则cosC=cos(
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| ||
| 10 |
点评:此题考查了正弦、余弦定理,两角和与差的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
下列结论错误的是( )
| A、命题“若p,则q”与命题“若非q,则非p”互为逆否命题 | ||||||
B、“sinx=
| ||||||
C、为得到函数y=sin(2x-
| ||||||
D、命题q:?x∈R,sinx-cosx≤
|
设z=2x+y,其中变量x,y满足条件
,则z的最小值为( )
|
| A、3 | B、6.4 | C、9.6 | D、12 |
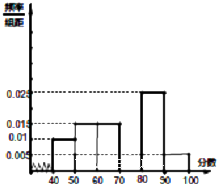 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如下部分频率颁布直方图,观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如下部分频率颁布直方图,观察图形的信息,回答下列问题: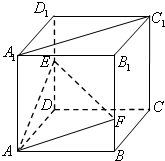 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.