题目内容
设全集U=R，M={x|x＜-2或x＞2}，N={x|x＜1或x≥3}都是U的子集，则图中阴影部分所表示的集合是（ ）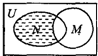
| A、{x|-2≤x＜1} |
| B、{x|-2≤x≤2} |
| C、{x|1＜x≤2） |
| D、{x|x＜2} |
考点：Venn图表达集合的关系及运算
专题：集合
分析：由图象可知阴影部分对应的集合为N∩（∁UM），然后根据集合的基本运算求解即可．
解答：
解：由Venn图可知阴影部分对应的集合为N∩（∁UM），
∵M={x|x＜-2或x＞2}，
∴∁UM={x|-2≤x≤2}，
即N∩（∁UM）={x|-2≤x＜1}
故选：A．
∵M={x|x＜-2或x＞2}，
∴∁UM={x|-2≤x≤2}，
即N∩（∁UM）={x|-2≤x＜1}
故选：A．
点评：本题主要考查集合的基本运算，利用图象先确定集合关系是解决本题的关键，比较基础．
练习册系列答案
相关题目
分别在两个平面内的两条直线的位置关系是（ ）
| A、异面 | B、相交 |
| C、平行 | D、以上都有可能 |
已知集合M={x|-1＜x＜2}，N={x|x＜a}，若M⊆N，则实数a的取值范围是（ ）
| A、（2，+∞） |
| B、[2，+∞） |
| C、（-∞，-1） |
| D、（-∞，-1] |
已知z1=2-i，
=-1-i，在复平面内复数
所对应的点位于（ ）
. |
| z2 |
| z1 |
| z2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
| sin2002°sin2008°-cos6° |
| sin2002°cos2008°+sin6° |
A、-
| ||
B、
| ||
| C、-tan28° | ||
| D、tan28° |