题目内容
已知集合M={x|-1＜x＜2}，N={x|x＜a}，若M⊆N，则实数a的取值范围是（ ）
| A、（2，+∞） |
| B、[2，+∞） |
| C、（-∞，-1） |
| D、（-∞，-1] |
考点：集合的包含关系判断及应用
专题：集合
分析：由集合M={x|-1＜x＜2}，N={x|x＜a}，M⊆N，由集合包含关系的定义比较两个集合的端点可直接得出结论
解答：
解：∵集合M={x|-1＜x＜2}，N={x|x＜a}，M⊆N，
∴a≥2，
实数a的取值范围是[2，+∞）
故选B．
∴a≥2，
实数a的取值范围是[2，+∞）
故选B．
点评：本题考查集合关系中的参数取值问题解题的关键是根据题设中的条件作出判断，得到参数所满足的不等式，从而得到其取值范围，此类题的求解，可以借助数轴，避免出错．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
正方体中两条面对角线的位置关系是（ ）
| A、平行 | B、异面 |
| C、相交 | D、平行、相交、异面都有可能 |
“x＞1”是“
＜1”的（ ）
| 1 |
| x |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设全集U=R，M={x|x＜-2或x＞2}，N={x|x＜1或x≥3}都是U的子集，则图中阴影部分所表示的集合是（ ）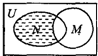
| A、{x|-2≤x＜1} |
| B、{x|-2≤x≤2} |
| C、{x|1＜x≤2） |
| D、{x|x＜2} |
已知A={x|y=x2-1}，B={y|y=x2-1}，则A∩B（ ）
| A、∅ | B、A | C、B | D、R |
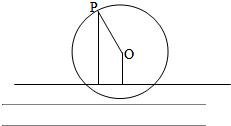如图是一个半径为3米的水轮，水轮圆心O距离水面2米，已知水轮每分钟转动四圈，水轮上的点P相对于水面的高度y（米）与时间x（秒）满足函数关系y=Asin（ωx+φ）+2（A＞0，ω＞0，φ∈（-